Implementacje algorytmów sortowania w Pythonie

Proces sortowania danych jest fundamentem wielu operacji w programowaniu. Efektywność tego procesu zależy od wyboru odpowiedniego algorytmu, a jego niewłaściwe zastosowanie może skutkować wydłużonym czasem realizacji.

W niniejszym opracowaniu przyjrzymy się różnorodnym technikom sortowania.

Przeanalizujemy algorytmy sortowania, prezentując ich implementację krok po kroku. Przykłady zostaną przedstawione w języku Python, jednak zrozumienie istoty każdego algorytmu pozwoli na jego adaptację do dowolnego języka programowania. Różnice będą sprowadzały się głównie do składni.

W tym przewodniku zaprezentujemy algorytmy, zaczynając od tych o najmniejszej efektywności, a kończąc na bardziej zaawansowanych rozwiązaniach. Proszę śledzić kolejne kroki i samodzielnie wdrażać przedstawione koncepcje.

Przejdźmy zatem do analizy poszczególnych algorytmów sortowania.

Sortowanie przez wstawianie

Sortowanie przez wstawianie to jedna z najprostszych metod sortowania, cechująca się łatwością implementacji. Mimo to, sortowanie dużych zbiorów danych przy jego użyciu jest czasochłonne i często nie jest to najlepszy wybór dla większych tablic.

Algorytm ten dzieli tablicę na dwie części: posortowaną i nieposortowaną.

Na początku procesu sortowania część posortowana zawiera jedynie pierwszy element. Kolejno, elementy z części nieposortowanej są wstawiane na właściwe pozycje w części posortowanej.

Prześledźmy na przykładzie, jak krok po kroku przebiega sortowanie przez wstawianie.

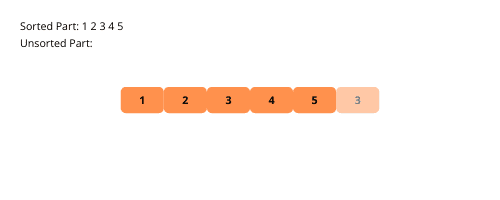
Oto sposób implementacji sortowania przez wstawianie:

• Zainicjuj tablicę przykładowymi danymi (liczbami całkowitymi).
• Przejdź iteracyjnie po tablicy, zaczynając od drugiego elementu.
  • Zapisz bieżący element i jego pozycję w zmiennych.
  • Utwórz pętlę, która przesuwa elementy w posortowanej części tablicy, dopóki nie znajdzie się właściwe miejsce dla bieżącego elementu (mniejszy element lub początek tablicy).
    • Przesuń element poprzedzający bieżącą pozycję o jedną pozycję w prawo.
    • Zmniejsz bieżącą pozycję.
  • Gdy pętla zakończy działanie (dojdzie do początku tablicy lub znajdzie mniejszy element), umieść bieżący element na zwolnionej pozycji.

Złożoność czasowa sortowania przez wstawianie wynosi O(n^2), a złożoność pamięciowa O(1).

To wszystko; tablica jest już posortowana. Poniżej znajduje się kod do uruchomienia. Jeśli Python nie jest zainstalowany, warto skorzystać z kompilatora online lub zapoznać się z przewodnikiem instalacji.

def insertion_sort(arr, n):
  for i in range(1, n):

  ## current position and element
  current_position = i
  current_element = arr[i]

  ## iteratin until
  ### it reaches the first element or
  ### the current element is smaller than the previous element
  while current_position > 0 and current_element <
  arr[current_position - 1]:
  ## updating the current element with previous element
  arr[current_position] = arr[current_position - 1]

  ## moving to the previous position
  current_position -= 1

  ## updating the current position element
  arr[current_position] = current_element

if __name__ == '__main__':
  ## array initialization
  arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
  insertion_sort(arr, 9)

  ## printing the array
  print(str(arr))

Sortowanie przez wybieranie

Sortowanie przez wybieranie, podobnie jak sortowanie przez wstawianie, również dzieli tablicę na część posortowaną i nieposortowaną. W każdej iteracji wybierany jest minimalny element z nieposortowanej części i przenoszony na koniec części posortowanej.

Poniżej przedstawiono ilustracje, które pomogą w zrozumieniu tego procesu.

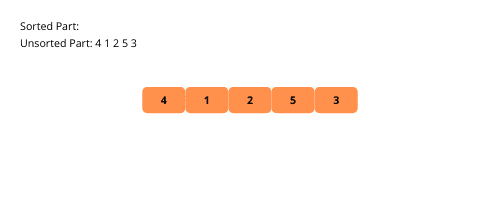
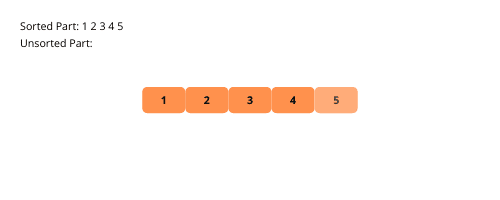
Oto jak zaimplementować sortowanie przez wybieranie:

• Zainicjuj tablicę przykładowymi danymi (liczbami całkowitymi).
• Przejdź iteracyjnie po tablicy.
  • Zapisz indeks minimalnego elementu.
  • Utwórz pętlę, która przechodzi od bieżącego elementu do końca tablicy.
    • Sprawdź, czy bieżący element jest mniejszy od elementu minimalnego.
    • Jeśli tak, zaktualizuj indeks elementu minimalnego.
  • Gdy pętla się zakończy, zamień bieżący element z elementem minimalnym.

Złożoność czasowa sortowania przez wybieranie wynosi O(n^2), a złożoność pamięciowa O(1).

Zachęcamy do samodzielnego zaimplementowania algorytmu, gdyż jest zbliżony do sortowania przez wstawianie. Kod znajduje się poniżej.

def selection_sort(arr, n):
  for i in range(n):

  ## to store the index of the minimum element
  min_element_index = i
  for j in range(i + 1, n):
  ## checking and replacing the minimum element index
  if arr[j] < arr[min_element_index]:
  min_element_index = j

  ## swaping the current element with minimum element
  arr[i], arr[min_element_index] = arr[min_element_index], arr[i]

if __name__ == '__main__':
  ## array initialization
  arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
  selection_sort(arr, 9)

  ## printing the array
  print(str(arr))

Sortowanie bąbelkowe

Sortowanie bąbelkowe to prosty algorytm, który polega na wielokrotnym porównywaniu i zamienianiu sąsiednich elementów, aż do uzyskania posortowanej tablicy.

Algorytm iteruje po tablicy i przesuwa bieżący element na kolejną pozycję, dopóki nie jest mniejszy od elementu następnego.

Ilustracje poniżej pomogą wizualnie zrozumieć działanie sortowania bąbelkowego.

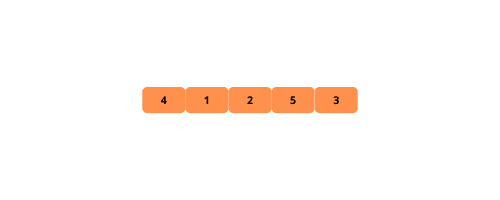
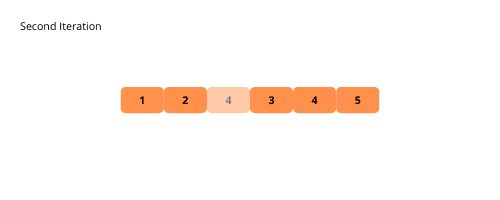
Oto jak zaimplementować sortowanie bąbelkowe:

• Zainicjuj tablicę przykładowymi danymi (liczbami całkowitymi).
• Przejdź iteracyjnie po tablicy.
• Przejdź iteracyjnie od 0 do n-i-1. Ostatnie „i” elementów jest już posortowane.
• Sprawdź, czy bieżący element jest większy od następnego.
• Jeśli tak, zamień te dwa elementy miejscami.

Złożoność czasowa sortowania bąbelkowego to O(n^2), a złożoność pamięciowa O(1).

Implementacja sortowania bąbelkowego jest stosunkowo prosta. Sprawdź poniższy kod.

def bubble_sort(arr, n):
  for i in range(n):
  ## iterating from 0 to n-i-1 as last i elements are already sorted
  for j in range(n - i - 1):
  ## checking the next element
  if arr[j] > arr[j + 1]:
  ## swapping the adjucent elements
  arr[j], arr[j + 1] = arr[j + 1], arr[j]

if __name__ == '__main__':
  ## array initialization
  arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
  bubble_sort(arr, 9)

  ## printing the array
  print(str(arr))

Sortowanie przez scalanie

Sortowanie przez scalanie to rekurencyjny algorytm, który jest bardziej efektywny niż poprzednio omówione algorytmy pod względem złożoności czasowej. Działa w oparciu o strategię „dziel i zwyciężaj”.

Algorytm dzieli tablicę na dwie połowy, sortuje je niezależnie, a następnie scala posortowane połówki w jedną, posortowaną tablicę.

Ze względu na rekurencyjny charakter, proces dzielenia tablicy trwa, dopóki nie uzyskamy najprostszych przypadków (tablic jednoelementowych).

Poniższa ilustracja przedstawia zasadę działania sortowania przez scalanie.

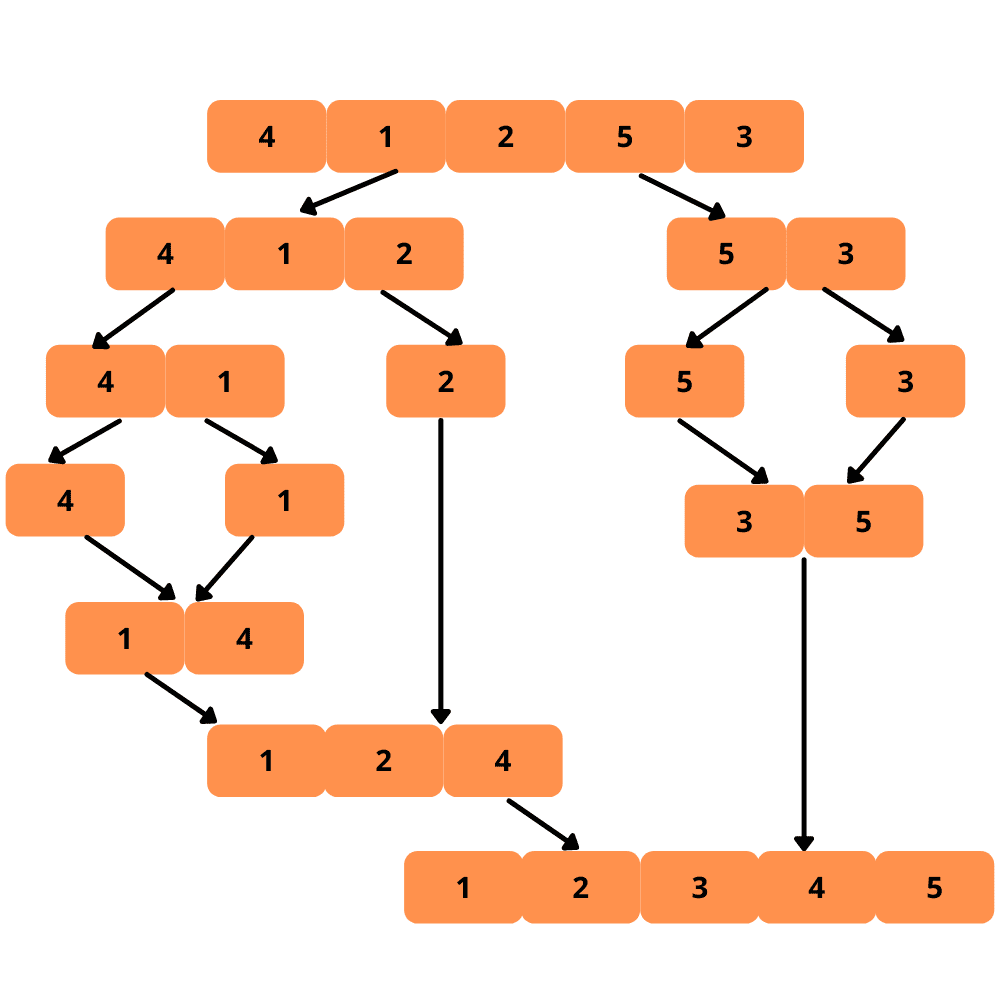
Oto jak zaimplementować sortowanie przez scalanie:

• Zainicjuj tablicę przykładowymi danymi (liczbami całkowitymi).
• Napisz funkcję `merge`, która łączy posortowane podtablice w jedną posortowaną tablicę. Funkcja przyjmuje tablicę oraz lewy, środkowy i prawy indeks jako argumenty.
  • Wyznacz długości lewej i prawej podtablic na podstawie podanych indeksów.
  • Skopiuj elementy z tablicy do odpowiednich tablic (lewej i prawej).
  • Przejdź iteracyjnie po obu podtablicach.
    • Porównaj dwa elementy z podtablic.
    • Umieść mniejszy element w tablicy wynikowej.
  • Sprawdź, czy pozostały jakieś elementy w obu podtablicach i dodaj je do tablicy.
• Napisz funkcję `merge_sort` z argumentami: tablicą, lewym i prawym indeksem.
  • Jeśli lewy indeks jest większy lub równy prawemu indeksowi, zakończ funkcję.
  • Znajdź środkowy punkt tablicy, aby podzielić ją na dwie połowy.
  • Rekurencyjnie wywołaj metodę `merge_sort` dla lewej i prawej połowy tablicy.
  • Po rekurencyjnych wywołaniach, scal posortowane połówki przy pomocy funkcji `merge`.

Złożoność czasowa sortowania przez scalanie wynosi O(n log n), a złożoność pamięciowa O(1).

Poniżej znajduje się kod implementujący algorytm sortowania przez scalanie.

def merge(arr, left_index, mid_index, right_index):
  ## left and right arrays
  left_array = arr[left_index:mid_index+1]
  right_array = arr[mid_index+1:right_index+1]

  ## getting the left and right array lengths
  left_array_length = mid_index - left_index + 1
  right_array_length = right_index - mid_index

  ## indexes for merging two arrays
  i = j = 0

  ## index for array elements replacement
  k = left_index

  ## iterating over the two sub-arrays
  while i < left_array_length and j < right_array_length:

  ## comapring the elements from left and right arrays
  if left_array[i] < right_array[j]:
  arr[k] = left_array[i]
  i += 1
  else:
  arr[k] = right_array[j]
  j += 1
  k += 1

  ## adding remaining elements from the left and right arrays
  while i < left_array_length:
  arr[k] = left_array[i]
  i += 1
  k += 1

  while j < right_array_length:
  j += 1
  k += 1

def merge_sort(arr, left_index, right_index):
  ## base case for recursive function
  if left_index >= right_index:
  return

  ## finding the middle index
  mid_index = (left_index + right_index) // 2

  ## recursive calls
  merge_sort(arr, left_index, mid_index)
  merge_sort(arr, mid_index + 1, right_index)

  ## merging the two sub-arrays
  merge(arr, left_index, mid_index, right_index)

if __name__ == '__main__':
  ## array initialization
  arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
  merge_sort(arr, 0, 8)

  ## printing the array
  print(str(arr))

Podsumowanie

Istnieje wiele innych algorytmów sortowania, jednak powyżej przedstawiono najczęściej wykorzystywane. Mam nadzieję, że proces nauki sortowania był interesujący.

W dalszej kolejności zachęcam do zapoznania się z algorytmami wyszukiwania.

Życzę owocnej nauki kodowania 🙂 👨‍💻