Samouczek dotyczący kodowania wywiadów

Proces porządkowania zbiorów danych jest kluczowym elementem w programowaniu aplikacji.

Ułatwia prezentację informacji oraz realizację operacji wyszukiwania. Z tego względu, każdy kompetentny specjalista ds. oprogramowania powinien posiadać wiedzę na temat metod sortowania tablic. W tym artykule przedstawione zostaną popularne algorytmy sortowania tablic w środowisku JavaScript.

Czym jest sortowanie i jakie ma znaczenie?

Źródło: Usuń rozpryski

Sortowanie to procedura systematycznego aranżowania danych zgodnie z określonym kryterium. To kryterium może ustalać porządek rosnący bądź malejący. Sortowanie list w JavaScript jest wartościowe, gdyż umożliwia bardziej klarowną wizualizację danych.

Przykładowo, użytkownik może preferować, aby pliki były ułożone chronologicznie, a towary według ceny. Jest również niezbędne w algorytmie wyszukiwania binarnego, który jest efektywny tylko dla danych, które są już posortowane.

Pomimo istnienia wbudowanych funkcji i bibliotek, które usprawniają proces sortowania danych, zrozumienie zasad działania tych algorytmów jest nadal ważne podczas rozmów rekrutacyjnych i przy pisaniu kodu niskopoziomowego.

Algorytmy sortowania tablic w JavaScript

Sortowanie bąbelkowe

Sortowanie bąbelkowe jest prawdopodobnie najłatwiejszym algorytmem do zrozumienia i zastosowania. Jego działanie polega na iteracyjnym przechodzeniu przez tablicę. W każdej iteracji, tablica jest przemierzana od początku do końca, gdzie porównywane są ze sobą dwa sąsiednie elementy. Jeśli elementy są w niewłaściwej kolejności, są zamieniane miejscami.

Wykonujemy n obiegów, gdzie n to ilość elementów tablicy. Po każdej iteracji, elementy na końcu tablicy są już uporządkowane. Algorytm sortowania liczb w kolejności rosnącej, w formie pseudokodu, przedstawia się następująco:

1. Niech n oznacza liczbę elementów w tablicy.
2. Wykonaj pętlę n razy, śledząc liczbę iteracji za pomocą zmiennej i (w każdej iteracji wykonaj następujące działania):
   a. Przejdź przez tablicę od drugiego elementu do elementu (n - i) - tego.
   b. Jeżeli poprzedni element jest większy niż element bieżący, zamień je miejscami.

Przekładając to na język JavaScript, kod będzie wyglądał następująco:

function sort(arr) {
    const n = arr.length;

    for (let i = 0; i < n; i++) {
        for (let j = 1; j < n - i; j++) {
            if (arr[j - 1] > arr[j]) {
                const temp = arr[j - 1];
                arr[j - 1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    
    return arr;
}

Aby dokładniej zrozumieć przebieg algorytmu, sugerowane jest dodanie poleceń console.log w obu pętlach, aby móc monitorować, jak zmienia się tablica w każdym obiegu.

W przedstawionym poniżej kodzie zmodyfikowano funkcję sortowania, dodając polecenia console.log do obu pętli. Dodatkowo stworzono niewielką, nieposortowaną tablicę, która następnie została posortowana za pomocą funkcji sortowania.

function sort(arr) {
    const n = arr.length;

    for (let i = 0; i < n; i++) {
	console.log(`Pass: ${i}`);

        for (let j = 1; j < n - i; j++) {
            if (arr[j - 1] > arr[j]) {
                const temp = arr[j - 1];
                arr[j - 1] = arr[j];
                arr[j] = temp;
            }
	
	    console.log(arr);
        }
    }
    
    return arr;
}

const array = [9, 2, 7, 4, 1];
sort(array);

console.log(array);

Wykonanie powyższego kodu poskutkuje wyświetleniem następującego rezultatu:

Sortowanie bąbelkowe ma złożoność obliczeniową Big O równą O(n ^ 2). Wynika to z faktu, że wykonuje n obiegów, a w każdym obiegu przechodzi przez całą tablicę. Dlatego jego efektywność spada wraz ze wzrostem liczby danych. Niemniej jednak, jego złożoność pamięciowa wynosi O(1), ponieważ modyfikacje tablicy odbywają się w miejscu.

Sortowanie przez wstawianie

Sortowanie przez wstawianie jest kolejnym popularnym algorytmem sortowania tablic w JavaScript. Zakładając, że celem jest posortowanie wartości w kolejności rosnącej, algorytm działa poprzez wybór elementu, który nazwiemy „num”. Następnie „num” jest przesuwany w lewo, dopóki każda wartość na lewo od niego nie będzie od niego mniejsza. Wszystkie elementy zostaną posortowane, jeśli powyższa procedura zostanie wykonana od drugiego do ostatniego elementu tablicy. Poniżej przedstawiono opis algorytmu w formie pseudokodu.

1. Niech n oznacza liczbę elementów w tablicy.
2. Wykonaj pętlę i od 1 do n - 1 (rozpocznij od drugiego elementu)
    a. Ustaw zmienną currentElement na array[i]
    b. Ustaw zmienną j na i - 1
    c. Dopóki j >= 0 i array[j] > current_element
       i. Przesuń array[j] do array[j+1]
       ii. Zmniejsz j o 1
    d. Ustaw array[j+1] na current_element

Poniżej zaprezentowano pseudokod zaimplementowany w JavaScript.

function insertionSort(array) {
  const n = array.length;

  for (let i = 1; i < n; i++) {
    const currentElement = array[i];
    let j = i - 1;

    while (j >= 0 && array[j] > currentElement) {
      array[j + 1] = array[j];
      j -= 1;
    }

    array[j + 1] = currentElement;
  }

  return array;
}

Analogicznie jak w przypadku sortowania bąbelkowego, dodanie console.log ułatwia wizualizację postępów algorytmu. Poniższy fragment kodu obrazuje działanie sortowania przez wstawianie.

function sort(array) {
    const n = array.length;

    for (let i = 1; i < n; i++) {
        const currentElement = array[i];
        let j = i - 1;
        console.log("Placing element:", currentElement);

        while (j >= 0 && array[j] > currentElement) {
            array[j + 1] = array[j];
            j -= 1;
        }

        array[j + 1] = currentElement;
        console.log("Placed it at position:", j + 1);
        console.log(array);
    }

    return array;
}

const array = [4, 1, 2, 5, 3];
sort(array);

Wykonanie powyższego fragmentu kodu da następujący wynik:

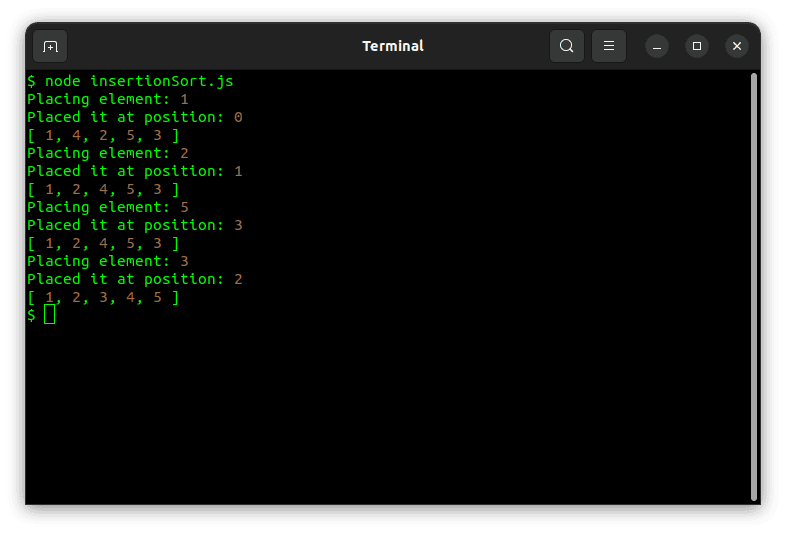
Sortowanie przez scalanie

Sortowanie przez wstawianie oraz sortowanie bąbelkowe charakteryzują się kwadratową złożonością czasową, natomiast sortowanie przez scalanie osiąga złożoność quasi-liniową, czyli O(n * log(n)).

Sortowanie przez scalanie bazuje na strategii „dziel i zwyciężaj”. Tablica jest cyklicznie dzielona na mniejsze podtablice, aż każda z nich będzie zawierała jeden element. Po dokonaniu podziału, podtablice są ponownie scalane.

Proces podziału jest rekurencyjny, co umożliwia późniejsze połączenie elementów.

Podczas ponownego łączenia, podtablice są scalane w odpowiedniej kolejności. Scalanie odbywa się w analogiczny sposób, jak scalanie dwóch posortowanych tablic. Algorytm tego procesu w formie pseudokodu przedstawiono poniżej:

1. Jeżeli długość tablicy wynosi 1 lub mniej, zwróć tablicę (przypadek bazowy).
2. Znajdź środkowy indeks:
   a. Ustaw zmienną mid jako zaokrągloną w dół wartość (długość tablicy / 2)
3. Podziel tablicę na dwie podtablice:
   a. Utwórz lewą podtablicę (leftArray) i skopiuj do niej pierwszą połowę tablicy (od indeksu 0 do mid)
   b. Utwórz prawą podtablicę (rightArray) i skopiuj do niej drugą połowę tablicy (od indeksu mid+1 do końca)
4. Rekurencyjnie wywołaj MergeSort na lewej podtablicy (leftArray)
5. Rekurencyjnie wywołaj MergeSort na prawej podtablicy (rightArray)
6. Scal dwie posortowane podtablice:
   a. Utwórz pustą tablicę wynikową (resultArray)
   b. Dopóki zarówno lewa (leftArray), jak i prawa (rightArray) podtablica nie są puste:
      i. Jeżeli pierwszy element w lewej podtablicy jest mniejszy lub równy pierwszemu elementowi w prawej podtablicy, dodaj go do tablicy wynikowej (resultArray)
      ii. W przeciwnym wypadku, dodaj pierwszy element z prawej podtablicy do tablicy wynikowej (resultArray)
   c. Dodaj do tablicy wynikowej (resultArray) pozostałe elementy lewej podtablicy (jeśli takie istnieją)
   d. Dodaj do tablicy wynikowej (resultArray) pozostałe elementy prawej podtablicy (jeśli takie istnieją)
7. Zwróć tablicę wynikową (resultArray)

Implementacja w JavaScript dałaby następujące wyniki:

function sort(array) {

	// Przypadek bazowy, w którym zatrzymujemy dzielenie tablicy
	if (array.length == 1) {
		return array;
	}

	// Znalezienie środkowego punktu tablicy
	const m = Math.round(array.length / 2);

	// Podział tablicy na dwie połowy
	const leftUnsorted = array.slice(0, m);
	const rightUnsorted = array.slice(m);

	// Rekurencyjne wywołanie sortowania przez scalanie
	const leftSorted = sort(leftUnsorted);
	const rightSorted = sort(rightUnsorted);

	// Zwróć posortowaną tablicę po scaleniu
	return merge(leftSorted, rightSorted);
}

function merge(left, right) {
	// Scal dwie posortowane listy
	let result = [];
	let leftIndex = 0;
	let rightIndex = 0;

	while (leftIndex < left.length && rightIndex < right.length) {
		if (left[leftIndex] < right[rightIndex]) {
			result.push(left[leftIndex]);
			leftIndex += 1;
		} else {
			result.push(right[rightIndex]);
			rightIndex += 1;
		}
	}

	return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}

Po uruchomieniu kodu z przykładową tablicą, powinien on działać poprawnie.

Szybkie sortowanie

Podobnie jak sortowanie przez scalanie, szybkie sortowanie wykorzystuje strategię „dziel i zwyciężaj”. Algorytm wyznacza element osiowy (pivot). Następnie przesuwa wszystkie elementy większe od osi na prawo, a mniejsze na lewo. Po zakończeniu tego etapu, element osiowy znajduje się już na właściwej pozycji.

W celu przesunięcia elementów względem osi, algorytm inicjalnie przesuwa element osiowy na koniec tablicy.

Po tym przesunięciu, za pomocą wskaźnika, przeszukujemy tablicę od lewej strony, wyszukując pierwszą wartość większą od osi. Równocześnie, za pomocą kolejnego wskaźnika, przeszukujemy tablicę od prawej strony, szukając pierwszej wartości mniejszej od osi. Po zlokalizowaniu obu wartości, zamieniamy je miejscami. Procedurę tę kontynuujemy, dopóki wskaźnik z lewej strony nie znajdzie się na pozycji większej niż wskaźnik z prawej strony.

Gdy proces się zakończy, zamieniamy większą z dwóch ostatnio zamienionych wartości z osią. W tym momencie oś jest już na właściwej pozycji; liczby mniejsze od niej znajdują się po lewej stronie, a większe po prawej.

Cała procedura jest powtarzana rekurencyjnie dla podtablic z lewej i prawej strony osi, dopóki w podtablicach nie zostanie tylko jeden element.

Poniżej przedstawiono pseudokod szybkiego sortowania:

1. Jeżeli lewyWskaźnik jest mniejszy od prawegoWskaźnika:
    a. Wybierz element osiowy z tablicy
    b. Przesuń elementy tak, aby elementy mniejsze były po lewej, a większe po prawej stronie:
    c. Rekurencyjnie wywołaj QuickSort na lewej podtablicy
    d. Rekurencyjnie wywołaj QuickSort na prawej podtablicy

A oto implementacja w JavaScript:

function sort(array, low, high) {
    if (low < high) {
        // Wybierz indeks osi i podziel tablicę
        const pivotIndex = move(array, low, high);

        // Rekurencyjnie posortuj podtablice po lewej i prawej stronie osi
        sort(array, low, pivotIndex - 1);
        sort(array, pivotIndex + 1, high);
    }
}

function move(array, low, high) {
    // Wybierz element osiowy (w tym przypadku, ostatni element)
    const pivotElement = array[high];

    // Zainicjuj indeks dla mniejszego elementu
    let i = low - 1;

    for (let j = low; j < high; j++) {
        // Jeżeli bieżący element jest mniejszy lub równy osi, zamień go z elementem na pozycji i+1
        if (array[j] <= pivotElement) {
            i += 1;
            const temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
    }

    // Zamień element osiowy na jego właściwą pozycję
    const temp = array[i];
    array[i] = array[j];
    array[j] = temp;

    // Zwróć indeks elementu osiowego
    return i + 1;
}

Sortowanie przykładowej tablicy za pomocą szybkiego sortowania w Node.js powinno dać następujący rezultat:

W najlepszym przypadku, szybkie sortowanie osiąga quasi-liniową złożoność czasową. Zapotrzebowanie na pamięć w trybie szybkiego sortowania również skaluje się logarytmicznie. Dlatego jest stosunkowo efektywne w porównaniu do innych algorytmów sortowania tablic w JavaScript.

Wskazówki na temat rozmów kwalifikacyjnych dotyczących kodowania

❇️ Kluczem do sukcesu jest praktyka. Pomaga nie tylko w opanowaniu różnych algorytmów, ale przede wszystkim w rozwijaniu umiejętności rozwiązywania problemów i logicznego myślenia. Możesz trenować swoje umiejętności na platformach takich jak Leetcode i AlgoExpert.

❇️ Staraj się najpierw samodzielnie rozwiązać problem. Nie przechodź od razu do gotowego rozwiązania, ponieważ samodzielne próby rozwiązywania problemów rozwijają Twoje umiejętności w tym zakresie.

❇️ Jeśli problem sprawia trudności przez dłuższy czas, zapoznaj się z rozwiązaniem; nawet na tej podstawie można się wiele nauczyć. Większość platform edukacyjnych udostępnia rozwiązania. ChatGPT lub Google Bard mogą być również pomocne w wyjaśnianiu trudnych zagadnień.

❇️ Nie zaczynaj od razu pisać kodu; wcześniej przeanalizuj problem i przemyśl rozwiązanie. Tworzenie pseudokodu jest dobrym sposobem na szybkie notowanie pomysłów.

Podsumowanie

W tym artykule przedstawiliśmy najpopularniejsze algorytmy sortowania. Jednak nauka wszystkich na raz może wydawać się przytłaczająca. Dlatego zaleca się korzystanie z różnych źródeł wiedzy, a nie poleganie wyłącznie na jednym. Życzymy udanego kodowania!

Następnie sprawdźmy, jak działa funkcja sortowania w języku Python.