Ściągawka Big O: objaśniona na przykładach w języku Python

Analiza Big O to metoda oceny i porównywania efektywności algorytmów. Pozwala na identyfikację najbardziej wydajnych i skalowalnych rozwiązań. Ten artykuł stanowi kompendium wiedzy o notacji Big O, wyjaśniając wszystkie kluczowe aspekty.

Czym jest analiza Big O?

Analiza Big O to technika służąca do określania, jak efektywnie algorytmy radzą sobie ze wzrostem ilości przetwarzanych danych. Innymi słowy, bada, jak zmienia się wydajność algorytmu wraz ze wzrostem rozmiaru danych wejściowych.

Wydajność w tym kontekście odnosi się do stopnia wykorzystania zasobów systemowych podczas generowania wyników. Głównymi zasobami, które analizujemy, są czas obliczeń i zajętość pamięci.

Podczas analizy Big O staramy się odpowiedzieć na następujące pytania:

• Jak zmienia się zapotrzebowanie algorytmu na pamięć wraz ze wzrostem ilości danych wejściowych?
• Jak długo trwa obliczenie wyniku przez algorytm w miarę zwiększania się ilości danych?

Odpowiedź na pierwsze pytanie opisuje złożoność pamięciową algorytmu, a odpowiedź na drugie – jego złożoność czasową. Do wyrażenia tych zależności używamy specjalnego zapisu zwanego notacją Big O, którą szczegółowo omówimy w dalszej części artykułu.

Wymagania wstępne

Zanim przejdziesz dalej, powinieneś wiedzieć, że aby w pełni wykorzystać informacje zawarte w tym artykule, powinieneś mieć podstawową wiedzę z zakresu algebry. Dodatkowo, ponieważ będziemy korzystać z przykładów w języku Python, znajomość tego języka będzie bardzo pomocna. Nie jest jednak wymagana szczegółowa wiedza, ponieważ nie będziemy pisać rozbudowanego kodu.

Jak przeprowadzić analizę Big O?

W tej części omówimy, jak prawidłowo przeprowadzić analizę Big O.

Pamiętaj, że efektywność algorytmu zależy od struktury danych wejściowych. Algorytmy sortowania są najszybsze, gdy dane są już posortowane, co stanowi najlepszy scenariusz. Te same algorytmy działają najwolniej w przypadku danych posortowanych w odwrotnej kolejności – to najgorszy scenariusz.

Podczas analizy Big O bierzemy pod uwagę tylko najgorszy scenariusz.

Analiza złożoności pamięciowej

Zacznijmy od omówienia analizy złożoności pamięciowej. Skupiamy się na tym, jak dodatkowa ilość pamięci wykorzystywana przez algorytm zmienia się wraz ze wzrostem danych wejściowych.

Na przykład, poniższa funkcja wykorzystuje rekurencję do iteracji od n do zera. Jej złożoność pamięciowa jest wprost proporcjonalna do n. Dzieje się tak, ponieważ wraz ze wzrostem n, zwiększa się liczba wywołań funkcji na stosie wywołań. Zatem ma złożoność O(n).

def loop_recursively(n):
    if n == -1:
        return
    else:
        print(n)
        loop_recursively(n - 1)

Lepszym rozwiązaniem byłaby jednak następująca implementacja:

def loop_normally(n):
    count = n
    while count >= 0:
        print(count)
        count =- 1

W powyższym algorytmie tworzymy tylko jedną zmienną pomocniczą i używamy jej do iteracji. Nawet gdy n będzie rosło, będziemy używać tylko jednej dodatkowej zmiennej. Dlatego algorytm ma stałą złożoność pamięciową, oznaczoną jako „O(1)”.

Porównując złożoność pamięciową tych dwóch algorytmów, widzimy, że pętla while jest bardziej efektywna niż rekurencja. To właśnie jest celem analizy Big O: określenie, jak algorytmy zachowują się przy większych zestawach danych wejściowych.

Analiza złożoności czasowej

Analizując złożoność czasową, nie interesuje nas całkowity czas wykonania algorytmu. Bardziej interesuje nas, jak rośnie liczba wykonywanych kroków obliczeniowych. Dzieje się tak, ponieważ rzeczywisty czas zależy od wielu czynników systemowych i losowych. Dlatego skupiamy się na wzroście liczby kroków, zakładając, że każdy z nich trwa tyle samo czasu.

Aby zilustrować analizę złożoności czasowej, rozważmy następujący przykład: Mamy listę użytkowników, gdzie każdy ma unikalny identyfikator i nazwę. Naszym zadaniem jest napisanie funkcji, która zwraca nazwę użytkownika na podstawie jego identyfikatora. Możemy to zrobić w następujący sposób:

users = [
    {'id': 0, 'name': 'Alice'},
    {'id': 1, 'name': 'Bob'},
    {'id': 2, 'name': 'Charlie'},
]

def get_username(id, users):
    for user in users:
        if user['id'] == id:
            return user['name']
    return 'User not found'

get_username(1, users)

Mając listę użytkowników, algorytm przegląda ją po kolei, aż znajdzie użytkownika z odpowiednim identyfikatorem. Jeśli mamy trzech użytkowników, algorytm wykona trzy iteracje. Dla dziesięciu użytkowników wykona dziesięć iteracji.

Liczba kroków jest zatem liniowo i wprost proporcjonalna do liczby użytkowników. Stąd, nasz algorytm ma liniową złożoność czasową. Możemy jednak go ulepszyć.

Załóżmy, że zamiast listy, użytkowników przechowujemy w słowniku. Wtedy nasz algorytm wyglądałby tak:

users = {
    '0': 'Alice',
    '1': 'Bob',
    '2': 'Charlie'
}

def get_username(id, users):
     if id in users:
         return users[id]
     else:
         return 'User not found'

get_username(1, users)

W przypadku tego algorytmu, mając trzech użytkowników, wykonamy kilka kroków, aby uzyskać nazwę użytkownika. Załóżmy, że mamy dziesięciu. Nadal wykonamy tyle samo kroków, co wcześniej. Wraz ze wzrostem liczby użytkowników, liczba kroków potrzebnych do znalezienia użytkownika pozostaje stała.

Ten algorytm ma więc stałą złożoność. Niezależnie od liczby użytkowników, liczba wykonanych kroków jest zawsze taka sama.

Co to jest notacja Big O?

W poprzedniej sekcji omawialiśmy, jak określać złożoność czasową i pamięciową algorytmów. Do opisu używaliśmy takich słów jak liniowa i stała. Innym sposobem opisu złożoności jest użycie notacji Big O.

Notacja Big O to sposób na reprezentowanie złożoności pamięciowej lub czasowej algorytmu. Notacja jest prosta: składa się z litery O, po której następują nawiasy. Wewnątrz nawiasów zapisujemy funkcję n, która odzwierciedla daną złożoność.

Złożoność liniową reprezentuje n, zatem zapisujemy ją jako O(n) (czytamy jako „O od n”). Stałą złożoność reprezentuje 1, zatem zapisujemy ją jako O(1).

Istnieje więcej szczegółów, które omówimy w następnej sekcji. Ogólnie, aby zapisać złożoność algorytmu, należy wykonać następujące kroki:

1. Spróbuj opracować funkcję matematyczną n, f(n), gdzie f(n) to ilość wykorzystanej pamięci lub liczba kroków obliczeniowych wykonywanych przez algorytm, a n to rozmiar danych wejściowych.
2. Wybierz najbardziej dominujący składnik tej funkcji. Kolejność dominacji różnych składników, od najbardziej dominującego do najmniej dominującego, wygląda następująco: silnia, wykładnicza, wielomianowa, kwadratowa, liniowo-logarytmiczna, liniowa, logarytmiczna i stała.
3. Usuń wszystkie współczynniki z wybranego składnika.

Wynikiem tych kroków jest termin, który wpisujemy w nawiasach.

Przykład:

Rozważmy następującą funkcję w Pythonie:

users = [
    'Alice',
    'Bob',
    'Charlie'
]

def print_users(users):
    number_of_users = len(users)
    print("Total number of users:", number_of_users)

    for i in number_of_users:
        print(i, end=': ')
        print(user)

Teraz obliczymy złożoność czasową tego algorytmu w notacji Big O.

Najpierw tworzymy funkcję matematyczną f(n), która reprezentuje liczbę kroków obliczeniowych wykonywanych przez algorytm. Pamiętamy, że n reprezentuje rozmiar danych wejściowych.

W naszym kodzie funkcja wykonuje dwa kroki: jeden w celu obliczenia liczby użytkowników, a drugi, aby wyświetlić tę liczbę. Następnie, dla każdego użytkownika wykonuje dwa kolejne kroki: jeden, aby wyświetlić indeks, a drugi, aby wyświetlić nazwę użytkownika.

Funkcję, która najlepiej reprezentuje liczbę wykonanych kroków obliczeniowych, można zapisać jako f(n) = 2 + 2n, gdzie n to liczba użytkowników.

W drugim kroku wybieramy najbardziej dominujący składnik. 2n jest składnikiem liniowym, a 2 jest składnikiem stałym. Składnik liniowy dominuje nad stałym, zatem wybieramy 2n.

Nasza funkcja przyjmuje teraz postać f(n) = 2n.

Ostatnim krokiem jest wyeliminowanie współczynników. W naszej funkcji mamy współczynnik 2. Eliminujemy go. Funkcja staje się f(n) = n. To właśnie ten termin wpisujemy w nawiasach.

Zatem złożoność czasowa naszego algorytmu wynosi O(n), czyli złożoność liniowa.

Różne złożoności Big O

Ostatnia część naszego kompendium Big O przedstawia różne typy złożoności wraz z ich wykresami.

#1. Stała

Złożoność stała oznacza, że algorytm wykorzystuje stałą ilość pamięci (w analizie złożoności pamięciowej) lub wykonuje stałą liczbę kroków (w analizie złożoności czasowej). Jest to najbardziej optymalny przypadek, ponieważ algorytm nie potrzebuje dodatkowej pamięci ani czasu w miarę wzrostu danych wejściowych. Jest więc bardzo skalowalny.

Złożoność stała jest oznaczana jako O(1). Nie zawsze jest możliwe napisanie algorytmów o stałej złożoności.

#2. Logarytmiczna

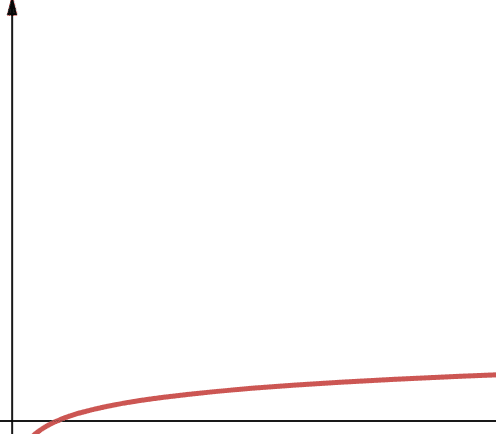
Złożoność logarytmiczna jest reprezentowana przez O(log n). Należy pamiętać, że jeśli podstawa logarytmu nie jest określona w informatyce, przyjmujemy, że wynosi ona 2.

Zatem log n to log₂n. Funkcje logarytmiczne rosną początkowo szybko, a następnie zwalniają. Oznacza to, że skalują się i działają efektywnie wraz ze wzrostem n.

#3. Liniowa

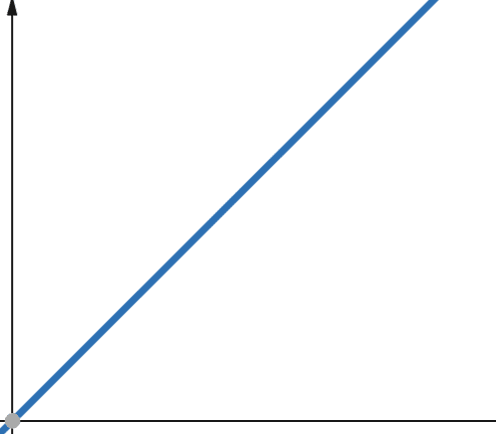
W funkcjach liniowych, jeśli zmienna niezależna skaluje się o współczynnik p, to zmienna zależna skaluje się o ten sam współczynnik p.

Funkcja o złożoności liniowej rośnie więc o taki sam współczynnik, jak rozmiar danych wejściowych. Jeśli rozmiar danych wejściowych podwoi się, zwiększy się również liczba kroków obliczeniowych i zużycie pamięci. Złożoność liniowa jest reprezentowana przez symbol O(n).

#4. Liniowo-logarytmiczna

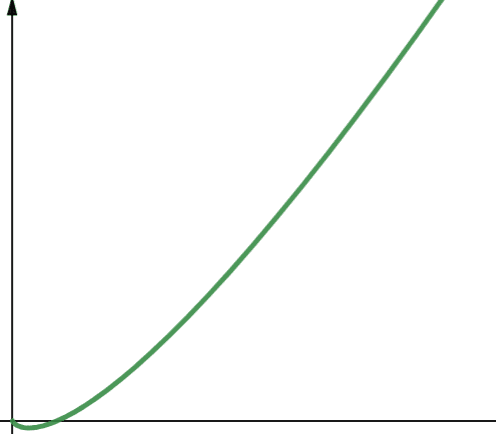
O(n * log n) reprezentuje funkcje liniowo-logarytmiczne. Funkcja liniowo-logarytmiczna to iloczyn funkcji liniowej i funkcji logarytmicznej. Zatem funkcja liniowo-logarytmiczna daje nieco większe wartości niż funkcja liniowa, gdy log n jest większe niż 1. Dzieje się tak, ponieważ n rośnie po pomnożeniu przez liczbę większą niż 1.

Log n jest większe niż 1 dla wszystkich wartości n większych niż 2 (pamiętaj, że log n to log₂n). Dlatego dla dowolnej wartości n większej niż 2, funkcje liniowo-logarytmiczne są mniej skalowalne niż funkcje liniowe. W większości przypadków n jest większe niż 2. Zatem funkcje liniowo-logarytmiczne są generalnie mniej skalowalne niż funkcje logarytmiczne.

#5. Kwadratowa

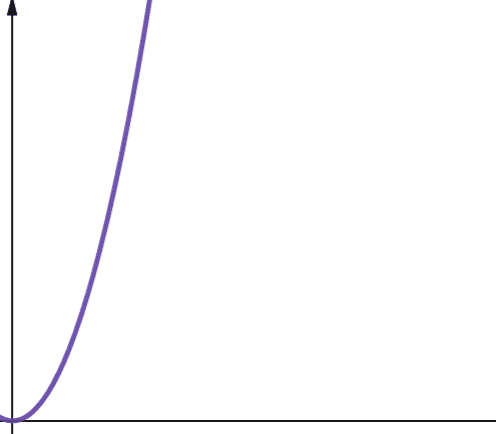
Złożoność kwadratowa jest reprezentowana przez O(n²). Oznacza to, że jeśli rozmiar danych wejściowych zwiększy się 10 razy, liczba wykonanych kroków lub zajęta pamięć wzrośnie 10² razy, czyli 100 razy. Nie jest to bardzo skalowalne i jak widać na wykresie, złożoność rośnie bardzo szybko.

Złożoność kwadratowa pojawia się w algorytmach, gdzie pętla jest wykonywana n razy, a dla każdej iteracji pętla jest wykonywana ponownie n razy, na przykład w sortowaniu bąbelkowym. Mimo że nie jest to idealne rozwiązanie, czasami nie ma innego wyjścia niż implementacja algorytmów o złożoności kwadratowej.

#6. Wielomianowa

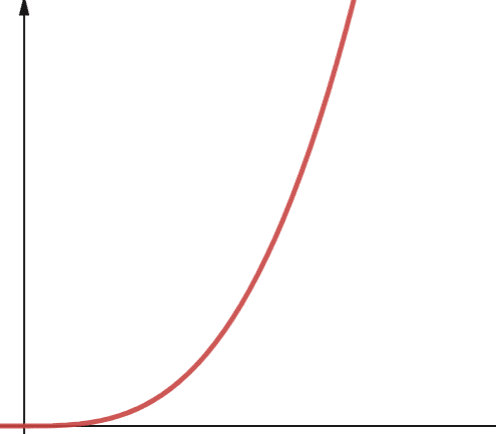
Algorytm o złożoności wielomianowej jest reprezentowany przez O(nᵖ), gdzie p to stała liczba całkowita. P reprezentuje rząd, do którego podnoszone jest n.

Złożoność ta pojawia się, gdy mamy do czynienia z kilkoma zagnieżdżonymi pętlami. Różnica między złożonością wielomianową a kwadratową polega na tym, że złożoność kwadratowa ma rząd 2, podczas gdy wielomianowa ma dowolną liczbę większą od 2.

#7. Wykładnicza

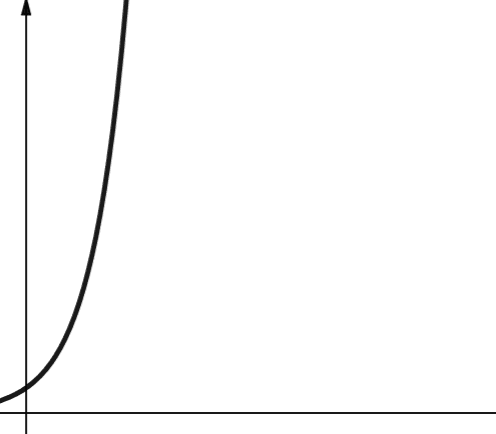
Złożoność wykładnicza rośnie jeszcze szybciej niż złożoność wielomianowa. W matematyce domyślną podstawą funkcji wykładniczej jest stała e (liczba Eulera). Jednak w informatyce domyślną podstawą jest 2.

Złożoność wykładnicza jest reprezentowana przez symbol O(2ⁿ). Gdy n wynosi 0, 2ⁿ wynosi 1. Ale gdy n wzrasta do 5, 2ⁿ wzrasta do 32. Zwiększenie n o jeden podwaja poprzednią liczbę. Dlatego funkcje wykładnicze nie są zbyt skalowalne.

#8. Silnia

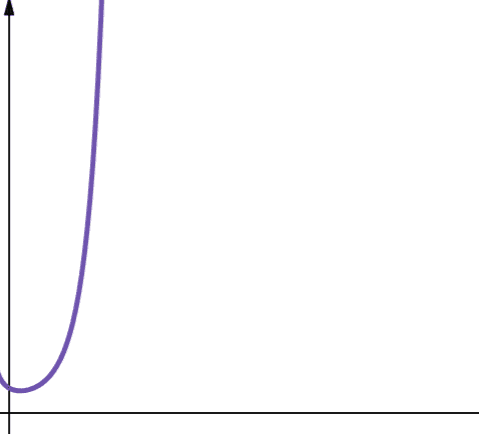
Złożoność silniowa jest reprezentowana przez symbol O(n!). Ta funkcja również rośnie bardzo szybko i dlatego nie jest skalowalna.

Podsumowanie

W tym artykule omówiliśmy analizę Big O i sposób jej obliczania. Przedstawiliśmy również różne typy złożoności, omawiając ich skalowalność.

Teraz możesz spróbować przećwiczyć analizę Big O na algorytmie sortowania w Pythonie.