Jak tworzyć tablice równomiernie rozmieszczonych liczb

W tym przewodniku krok po kroku dowiesz się, jak efektywnie wykorzystać funkcję `linspace()` z biblioteki NumPy w Pythonie do tworzenia tablic zawierających równo rozłożone wartości liczbowe.

Zgłębimy tajniki składni `linspace()`, prezentując przykłady, które pomogą Ci w pełni zrozumieć jej działanie i możliwości.

Pamiętaj, że aby w pełni skorzystać z tego samouczka, musisz mieć zainstalowanego Pythona oraz bibliotekę NumPy.

Jeśli nie masz jeszcze NumPy, nie martw się! Przygotowaliśmy krótki przewodnik, który przeprowadzi Cię przez proces instalacji.

Zaczynajmy naszą przygodę!

Instalacja i import NumPy

Zanim przejdziemy do sedna samouczka, szybko omówmy proces instalacji biblioteki NumPy.

⏩ Jeżeli masz już zainstalowane NumPy, możesz śmiało przejść do następnego rozdziału.

• Używając środowiska Google Colab – opartego na chmurze notatnika Jupyter – możesz natychmiast zaimportować NumPy i rozpocząć kodowanie. (to rozwiązanie jest zalecane w tym samouczku ✅)
• W przypadku pracy w lokalnym środowisku, rekomendujemy zainstalowanie dystrybucji Pythona Anaconda. Zawiera ona wiele preinstalowanych, przydatnych pakietów. Możesz pobrać instalator odpowiedni dla Twojego systemu operacyjnego. Cały proces instalacji trwa zaledwie kilka chwil. ⌛
• Jeżeli posiadasz już zainstalowanego Pythona, możesz zainstalować dystrybucję Anaconda, a do zarządzania pakietami użyć conda lub pip. Uruchom jedno z poniższych poleceń w wierszu poleceń Anaconda, aby zainstalować NumPy:

# Instalacja NumPy za pomocą conda
conda install numpy

# Instalacja NumPy za pomocą pip
pip install numpy

Kolejny krok to zaimportowanie numpy pod aliasem `np`, co pozwoli na odwoływanie się do biblioteki za pomocą skrótu `np`, zamiast pełnej nazwy, przy każdym odwołaniu do jej elementów:

import numpy as np

Teraz, używając notacji z kropką, będziemy mogli korzystać z każdej funkcji biblioteki NumPy w sposób: `np.nazwa_funkcji`.

Równomiernie rozmieszczone liczby – dlaczego są ważne?

Podczas pracy z tablicami NumPy często zachodzi potrzeba utworzenia tablicy z liczbami, które są równomiernie rozłożone w danym przedziale.

Zanim przejdziemy dalej, przyjrzyjmy się innej, podobnej funkcji: `np.arange()`.

Porównanie NumPy linspace() z NumPy arange()

Jeśli korzystałeś już wcześniej z NumPy, prawdopodobnie używałeś `np.arange()` do tworzenia tablic liczb w określonym zakresie.

Funkcja `np.arange(start, stop, step)` zwraca tablicę liczb, zaczynając od `start`, aż do `stop` (ale bez niej), z krokiem o wartości `step`. Domyślna wartość kroku to 1.

Jednak ustalenie odpowiedniej wartości kroku nie zawsze jest oczywiste. Zobaczmy, dlaczego tak się dzieje.

Na przykład, jeśli potrzebujesz 4 równomiernie rozłożonych liczb od 0 do 1, wiesz, że krok powinien wynosić 0,25. Używając `np.arange()`, nie otrzymasz jednak liczby 1 w tablicy. Będziesz musiał wybrać interwał, który wykracza poza pożądaną wartość stop.

Poniższy przykład ilustruje sytuacje, w których potrzebna jest określona liczba równomiernie rozłożonych punktów w przedziale [a, b].

Punkty równomiernie rozmieszczone w przedziale

Nasz pierwszy przykład, czyli 4 punkty w przedziale [0, 1] był dość prosty. Wiesz, że krok między punktami powinien wynosić 0,25.

Załóżmy, że masz nieco bardziej skomplikowany przykład – musisz wygenerować 7 równomiernie rozłożonych punktów od 1 do 33. W tym przypadku ustalenie wielkości kroku może nie być oczywiste od razu. Możesz jednak obliczyć wartość kroku manualnie.

Na szczęście `np.linspace()` znacznie upraszcza to zadanie!

Użyj funkcji `linspace()` z NumPy

Używając `np.linspace()`, wystarczy określić liczbę punktów, które chcesz uzyskać w danym przedziale, bez konieczności ustalania wielkości kroku. Otrzymasz tablicę z oczekiwanymi wartościami.

Mając to na uwadze, przejdźmy do omówienia składni `np.linspace()`.

Składnia NumPy linspace()

Poniżej przedstawiamy składnię funkcji `linspace()` z NumPy:

np.linspace(start, stop, num, endpoint, retstep, dtype, axis)

Na pierwszy rzut oka, powyższa składnia może wydawać się skomplikowana ze względu na liczbę parametrów.

Większość z tych parametrów jest jednak opcjonalna. W ciągu kilku minut zobaczysz, że składnia jest bardzo prosta.

Przeanalizujmy poszczególne parametry:

• `start` i `stop` to, odpowiednio, początek i koniec interwału. Zarówno `start`, jak i `stop` mogą być skalarami lub tablicami. W tym samouczku skupimy się na skalarnych wartościach początkowych i końcowych.
• `num` to liczba równomiernie rozłożonych punktów. Jest to parametr opcjonalny, a jego domyślna wartość to 50.
• `endpoint` również jest opcjonalnym parametrem, który może przyjmować wartość `True` lub `False`.
• Domyślna wartość to `True`, co oznacza, że punkt końcowy będzie domyślnie włączony do przedziału. Możesz jednak ustawić go na `False`, aby go wykluczyć.
• `retstep` to kolejny opcjonalny parametr logiczny. Ustawienie go na `True` spowoduje zwrócenie wartości kroku.
• `dtype` to typ danych liczb w tablicy. Typ jest zazwyczaj wywnioskowany jako `float`, dlatego nie musisz go podawać jawnie.
• `axis` to kolejny opcjonalny parametr, który określa oś, wzdłuż której mają być przechowywane liczby. Jest on istotny tylko wtedy, gdy wartości `start` i `stop` są tablicami.

▶️ Co zwraca `np.linspace()`?

Zwraca N-wymiarową tablicę z równomiernie rozmieszczonymi liczbami. Jeżeli parametr `retstep` jest ustawiony na `True`, zwraca również wartość kroku.

Na podstawie dotychczasowej dyskusji, uproszczona składnia `np.linspace()` wygląda następująco:

np.linspace(start, stop, num)

Powyższy kod zwróci tablicę `num` równomiernie rozłożonych liczb w przedziale `[start, stop]`.

Teraz, gdy znasz składnię, możemy przejść do praktycznych przykładów.

Tworzenie równomiernie rozłożonych tablic przy użyciu NumPy linspace()

#1. Jako pierwszy przykład, utworzymy tablicę z 20 równomiernie rozłożonymi liczbami w przedziale `[1, 5]`.

Wartości `start`, `stop` i `num` można określić za pomocą argumentów nazwanych, jak pokazano w poniższym kodzie:

import numpy as np
arr1 = np.linspace(start = 1,stop = 5,num = 20)
print(arr1)

# Wynik:
[1.         1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
 4.78947368 5.        ]

Zauważ, że liczby w tablicy zaczynają się od 1 i kończą na 5 – włączając obydwa punkty końcowe. Zwróć również uwagę, że wszystkie liczby, włącznie z 1 i 5, są reprezentowane jako `float`.

#2. W poprzednim przykładzie podaliśmy argumenty `start`, `stop` i `num` za pomocą nazw. Możemy też użyć argumentów pozycyjnych, podając same wartości we właściwej kolejności, jak pokazano poniżej:

import numpy as np
arr2 = np.linspace(1,5,20)
print(arr2)

# Wynik:
[1.         1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
 4.78947368 5.        ]

#3. Teraz utwórzmy kolejną tablicę, w której ustawimy parametr `retstep` na `True`.

W takim przypadku funkcja zwróci tablicę oraz wartość kroku. Możemy rozpakować te wartości do dwóch zmiennych: `arr3` (tablica) i `step_size` (wartość kroku).

Poniższy kod ilustruje, jak to zrobić.

import numpy as np
arr3, step_size = np.linspace(1,5,20,retstep = True)
print(arr3)

# Wynik:
[1.         1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
 4.78947368 5.        ]

# Wynik:
print(step_size)
0.21052631578947367

#4. W ostatnim przykładzie ustawimy parametr `endpoint` na `False` i zobaczymy, co się stanie.

import numpy as np
arr4 = np.linspace(1,5,20,endpoint = False)
print(arr4)

# Wynik:
[1.  1.2 1.4 1.6 1.8 2.  2.2 2.4 2.6 2.8 3.  3.2 3.4 3.6 3.8 
4.  4.2 4.4 4.6 4.8]

Zwrócona tablica zawiera 1, ale nie zawiera 5. Ostatnia wartość w tablicy to 4.8, ale wciąż mamy 20 liczb.

Do tej pory generowaliśmy tylko tablice z równomiernie rozłożonymi liczbami. W kolejnym rozdziale zwizualizujemy te liczby za pomocą wykresów.

Wizualizacja równomiernie rozłożonych liczb w przedziale

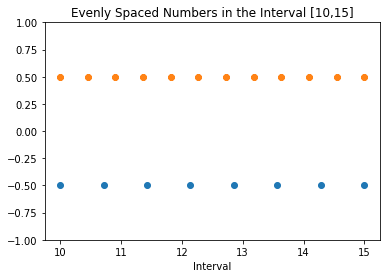
W tym rozdziale wybierzmy przedział `[10, 15]` jako zakres, który nas interesuje. Następnie użyjemy `np.linspace()` do wygenerowania dwóch tablic, odpowiednio z 8 i 12 punktami.

Na koniec wykorzystamy funkcje kreślenia z biblioteki `matplotlib`, aby przedstawić te dane na wykresie.

Aby ułatwić analizę, połączymy dwie tablice: `N1` = 8 i `N2` = 12 równomiernie rozłożonych punktów na różnych pozycjach wzdłuż osi y.

Poniższy fragment kodu prezentuje ten proces.

import numpy as np
import matplotlib.pyplot as plt

N1 = 8
N2 = 12

a = 10
b = 15

y1 = np.zeros(N1)
y2 = np.zeros(N2)

x1 = np.linspace(a, b, N1)
x2 = np.linspace(a, b, N2)

plt.plot(x1, y1-0.5, 'o')
plt.plot(x2, y2 + 0.5, 'o')

plt.ylim([-1, 1])

plt.title(f'Równomiernie rozmieszczone liczby w przedziale [{a},{b}]')
plt.xlabel('Przedział')

plt.show()

Generowanie równomiernie rozłożonych punktów może być szczególnie przydatne podczas pracy z funkcjami matematycznymi. Przekonamy się o tym w kolejnym rozdziale.

Wykorzystanie NumPy linspace() z funkcjami matematycznymi

Po wygenerowaniu tablicy równomiernie rozłożonych liczb za pomocą `np.linspace()`, możesz obliczyć wartości funkcji matematycznych w danym przedziale.

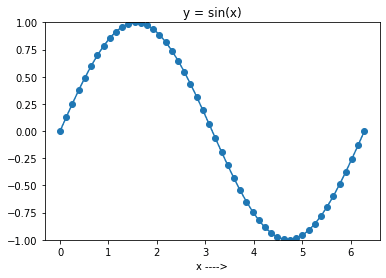
W poniższym kodzie najpierw generujemy 50 równomiernie rozłożonych punktów w przedziale od 0 do 2π. Następnie tworzymy tablicę `y`, używając funkcji `np.sin()` na tablicy `x`. Pamiętaj, że możesz pominąć parametr `num`, ponieważ jego domyślna wartość to 50. W przykładzie jednak użyliśmy go jawnie.

W kolejnym kroku możemy wykreślić funkcję sinus w przedziale `[0, 2π]`. W tym celu wykorzystamy bibliotekę `matplotlib`, tak jak w poprzednim przykładzie. Konkretnie, funkcja `plot()` z `matplotlib.pyplot` służy do tworzenia wykresu liniowego.

import numpy as np
import matplotlib.pyplot as plt

N = 50

a = 0.0
b = 2*np.pi

x = np.linspace(a, b, N)
y = np.sin(x)

plt.plot(x, y, marker = "o")

plt.ylim([-1, 1])
plt.title(f'y = sin(x)')
plt.xlabel('x ---->')

plt.show()

Teraz uruchom powyższy kod, ustawiając `N` na 10. Otrzymasz wykres przedstawiony na poniższym rysunku.

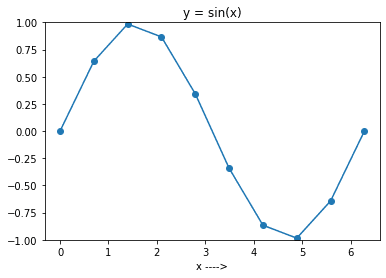
Jak widać, wykres nie jest zbyt gładki, ponieważ wybraliśmy tylko 10 punktów w przedziale.

Ogólnie rzecz biorąc, im większa liczba punktów, tym gładszy będzie wykres funkcji.

Podsumowanie

Oto podsumowanie, czego się nauczyliśmy:

• `np.linspace(start, stop, num)` zwraca tablicę `num` równomiernie rozłożonych liczb w przedziale `[start, stop]`.
• Ustaw opcjonalny parametr `endpoint` na wartość `False`, aby wykluczyć `stop`, i ustaw interwał na `[start, stop)`.
• Ustaw `retstep` na `True`, aby opcjonalnie uzyskać wartość kroku.
• Generuj tablice z równymi odstępami za pomocą `np.linspace()`, a następnie wykorzystuj je do obliczeń z funkcjami matematycznymi.

Mam nadzieję, że teraz rozumiesz, jak działa `np.linspace()`. Możesz uruchomić powyższe przykłady w notatniku Jupyter. Sprawdź nasz przewodnik po notatniku Jupyter lub inne alternatywne rozwiązania.

Do zobaczenia w kolejnym samouczku Pythona. Tymczasem, kontynuuj kodowanie! 😀