Ten artykuł przedstawi Ci krok po kroku, jak za pomocą języka Python napisać program, który zweryfikuje, czy dana liczba jest liczbą pierwszą.
Jeśli kiedykolwiek brałeś udział w konkursach programistycznych, na pewno spotkałeś się z zadaniem, które wymagało sprawdzenia, czy dana liczba jest liczbą pierwszą. W ciągu najbliższych minut nauczysz się, jak stworzyć optymalne rozwiązanie tego problemu.
W tym poradniku:
- Poznasz podstawowe informacje o liczbach pierwszych.
- Stworzysz kod w Pythonie, który sprawdzi, czy liczba jest liczbą pierwszą.
- Zoptymalizujesz kod, aby uzyskać algorytm o złożoności obliczeniowej O(√n).
Przejdźmy więc do sedna sprawy!
Definicja liczby pierwszej
Zacznijmy od wyjaśnienia, czym dokładnie jest liczba pierwsza.
W teorii liczb, liczba naturalna 'n’ jest uważana za liczbę pierwszą, jeżeli ma dokładnie dwa dzielniki: 1 i samą siebie (n). Pamiętasz z lekcji matematyki? Liczba 'i’ jest dzielnikiem liczby 'n’, jeśli 'i’ dzieli 'n’ bez reszty.
Poniższa tabela przedstawia przykłady liczb, ich dzielniki i informację, czy dana liczba jest liczbą pierwszą.
n Dzielniki Czy jest liczbą pierwszą? 1 1 Nie 2 1, 2 Tak 3 1, 3 Tak 4 1, 2, 4 Nie 7 1, 7 Tak 15 1, 3, 5, 15 Nie
Na podstawie powyższej tabeli możemy wywnioskować, że:
- 2 to najmniejsza liczba pierwsza.
- 1 jest dzielnikiem każdej liczby.
- Każda liczba 'n’ jest swoim własnym dzielnikiem.
Zatem 1 i 'n’ są dzielnikami trywialnymi dla dowolnej liczby 'n’. Liczba pierwsza nie powinna mieć innych dzielników poza tymi dwoma.
Oznacza to, że w przedziale od 2 do n-1, nie powinniśmy znaleźć żadnego dzielnika, który dzieliłby 'n’ bez reszty.
Algorytm O(n) do sprawdzania, czy liczba jest pierwsza w Pythonie
W tej części artykułu przekształcimy powyższe podejście w funkcję napisaną w Pythonie.
Możesz przejść przez wszystkie liczby od 2 do n-1, używając funkcji `range()` w Pythonie.
W Pythonie, `range(start, stop, step)` zwraca obiekt zakresu. Następnie możesz iterować po tym obiekcie, aby uzyskać sekwencję liczb od 'start’ do 'stop’ z krokiem 'step’.
Ponieważ potrzebujemy zbioru liczb całkowitych od 2 do n-1, możemy użyć `range(2, n)` w połączeniu z pętlą `for`.
Oto kroki, które musimy wykonać:
- Jeśli znajdziemy liczbę, która dzieli 'n’ bez reszty, możemy od razu stwierdzić, że liczba nie jest liczbą pierwszą.
- Jeśli przejdziemy przez cały zakres liczb od 2 do n-1 i nie znajdziemy żadnej liczby, która dzieli 'n’ bez reszty, to liczba jest liczbą pierwszą.
Funkcja Pythona sprawdzająca liczbę pierwszą
Bazując na powyższych założeniach, możemy zdefiniować funkcję `is_prime()` w następujący sposób:
def is_prime(n):
for i in range(2,n):
if (n%i) == 0:
return False
return True
Przeanalizujmy teraz tę funkcję.
- Funkcja `is_prime()` przyjmuje jako argument dodatnią liczbę całkowitą 'n’.
- Jeśli w podanym zakresie (2, n-1) znajdziemy dzielnik, funkcja zwróci `False`, ponieważ liczba nie jest pierwsza.
- Zwróci `True`, jeśli przejdziemy przez całą pętlę bez znalezienia dzielnika.
Wywołajmy teraz funkcję z różnymi argumentami i sprawdźmy, czy wyniki są prawidłowe.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True
Powyższe wyniki pokazują, że 2 i 11 są liczbami pierwszymi (funkcja zwraca `True`). Natomiast 8 i 9 nie są liczbami pierwszymi (funkcja zwraca `False`).
Optymalizacja funkcji `is_prime()` w Pythonie
Możemy wprowadzić tutaj niewielką optymalizację. Przyjrzyjmy się liście dzielników w poniższej tabeli.
Liczba Dzielniki 6 1, 2, 3, 6 10 1, 2, 5, 10 18 1, 2, 3, 6, 9, 18
Zauważ, że jedyny dzielnik liczby 'n’, który jest większy niż n/2, to sama liczba 'n’.
Oznacza to, że nie musimy iterować aż do n-1. Wystarczy, że sprawdzimy liczby do n/2.
Jeśli do n/2 nie znajdziemy żadnego nietrywialnego dzielnika, nie znajdziemy go również poza tym zakresem.
Zmodyfikujmy teraz funkcję `is_prime()`, aby sprawdzała dzielniki tylko w zakresie (2, n/2).
def is_prime(n):
for i in range(2,int(n/2)):
if (n%i) == 0:
return False
return True
Sprawdźmy teraz, czy funkcja działa poprawnie, wywołując ją kilka razy.
is_prime(9) # False is_prime(11) # True
Choć wydaje się, że dokonaliśmy optymalizacji, to ten algorytm nie jest bardziej efektywny niż poprzedni pod względem złożoności obliczeniowej. Oba algorytmy mają złożoność czasową O(n), czyli czas wykonania rośnie liniowo wraz z wartością 'n’.
Czy możemy zrobić to lepiej? Oczywiście, że tak!
▶️ Przejdź do następnej sekcji, aby dowiedzieć się, jak poprawić złożoność czasową sprawdzania, czy liczba jest pierwsza.
Algorytm O(√n) do sprawdzania, czy liczba jest pierwsza w Pythonie
Dzielniki liczb występują parami.
Jeśli 'a’ jest dzielnikiem liczby 'n’, to istnieje również dzielnik 'b’ taki, że a*b = n, czyli ab = n.
Sprawdźmy to na przykładzie.
W poniższej tabeli przedstawiono dzielniki liczby 18, które występują parami. Jeśli chcesz, możesz zweryfikować to na kilku innych liczbach.
Pamiętajmy, że √18 to w przybliżeniu 4.24.
W parach dzielników (a, b), jeżeli 'a’ jest mniejsze niż 4.24, to 'b’ jest większe niż 4.24. W tym przykładzie są to pary (2, 9) i (3, 6).
Dzielniki 18 w parach
Poniższy wykres przedstawia dzielniki liczby 18 umieszczone na osi liczbowej.
Jeśli liczba 'n’ jest idealnym kwadratem, będziemy mieli a = b = √n jako jeden z dzielników.
▶️ Spójrz na dzielniki liczby 36 w poniższej tabeli. Ponieważ 36 jest idealnym kwadratem, a = b = 6 jest jednym z dzielników. Dla wszystkich pozostałych par dzielników (a, b), a < 6 i b > 6.
Dzielniki 36 w parach
Podsumowując, mamy następujące:
- Każdą liczbę 'n’ można zapisać jako n = a*b
- Jeśli 'n’ jest idealnym kwadratem, to a = b = √n
- A jeśli a < b, to a < √n i b > √n.
- W przeciwnym przypadku, jeśli a > b, to a > √n i b < √n.
Zamiast więc przechodzić przez wszystkie liczby całkowite do n/2, możemy przeszukać zakres tylko do √n. Jest to o wiele bardziej wydajne niż poprzednie podejście.
Jak zmodyfikować algorytm `is_prime()` do O(√n)
Zoptymalizujmy teraz naszą funkcję, aby sprawdzić liczby pierwsze w Pythonie.
import math
def is_prime(n):
for i in range(2,int(math.sqrt(n))+1):
if (n%i) == 0:
return False
return True
Przeanalizujmy powyższą definicję funkcji:
- Aby obliczyć pierwiastek kwadratowy z liczby, zaimportujmy wbudowany moduł `math` w Pythonie i użyjmy funkcji `math.sqrt()`.
- Ponieważ 'n’ może nie być idealnym kwadratem, będziemy musieli przekonwertować go na liczbę całkowitą. Użyjemy funkcji `int(var)`, aby rzutować 'var’ na typ całkowity.
- Aby upewnić się, że faktycznie sprawdzamy zakres do √n, dodajemy jeden, ponieważ funkcja `range()` domyślnie wyklucza ostatni punkt zakresu.
Poniższy fragment kodu weryfikuje, czy funkcja `is_prime()` działa poprawnie.
is_prime(8) # False is_prime(15) # False is_prime(23) # True
W następnej sekcji utworzymy proste wykresy, aby wizualnie porównać O(n) i O(√n).
Wizualne porównanie O(n) i O(√n)
▶️ Uruchom poniższy fragment kodu w wybranym środowisku notebooka Jupyter.
import numpy as np
import seaborn as sns
import pandas as pd
n = 20
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
Powyższy kod pokazuje, jak narysować krzywe dla n i √n dla określonego zakresu wartości.
- Używamy funkcji `NumPy arange()`, aby utworzyć tablicę liczb.
- Następnie gromadzimy wartości n i √n (do 20, ale bez 20) w ramce danych pandas.
- Na koniec rysujemy wykres liniowy za pomocą funkcji `seaborn.lineplot()`.
Z poniższego wykresu widać, że √n jest znacznie mniejsze niż n.
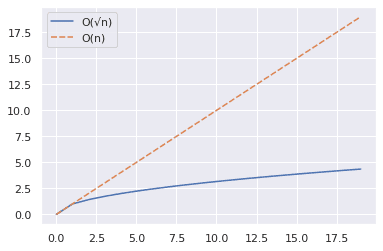
Zwiększmy teraz zakres do 2000 i powtórzmy te same kroki co powyżej.
import numpy as np
import seaborn as sns
import pandas as pd
n = 2000
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
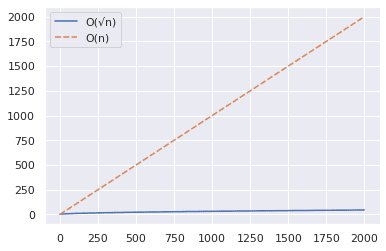
Z powyższego wykresu możemy wywnioskować, że algorytm O(√n) jest znacznie szybszy podczas sprawdzania, czy duża liczba jest liczbą pierwszą.
Oto krótki przykład: 2377 to liczba pierwsza – sprawdź to! 😀
Podejście O(n) wymagałoby około 2000 kroków, podczas gdy algorytm O(√n) pozwoli uzyskać odpowiedź w zaledwie 49 krokach. ✅
Podsumowanie
⏳ Czas na krótkie podsumowanie.
- Aby sprawdzić, czy liczba jest liczbą pierwszą, naiwne podejście polega na przejściu przez wszystkie liczby z zakresu (2, n-1). Jeśli nie znajdziemy dzielnika, który dzieli 'n’, to 'n’ jest liczbą pierwszą.
- Ponieważ jedyny dzielnik 'n’ większy niż n/2 to sama liczba 'n’, wystarczy przeszukać zakres do n/2.
- Oba powyższe podejścia mają złożoność czasową O(n).
- Ponieważ dzielniki liczb występują parami, możemy przeszukać zakres tylko do √n. Ten algorytm jest dużo szybszy niż O(n), a zysk jest szczególnie widoczny przy sprawdzaniu, czy duża liczba jest liczbą pierwszą.
Mam nadzieję, że rozumiesz, jak sprawdzić, czy liczba jest liczbą pierwszą w Pythonie. W następnym kroku możesz zapoznać się z naszym poradnikiem dotyczącym operacji na ciągach w Pythonie, gdzie dowiesz się, jak sprawdzać, czy łańcuchy są palindromami, anagramami i nie tylko.
Do zobaczenia w kolejnym poradniku. Do tego czasu życzę Ci miłego kodowania! 👩🏽💻