Poznaj istotę eksploracyjnej analizy danych, kluczowego etapu w procesie analizy, który umożliwia odkrywanie tendencji i schematów w zbiorach informacji. Wykorzystuje ona statystyki podsumowujące oraz wizualizacje graficzne, aby kompleksowo przedstawić dane.
Jak każdy projekt, analiza danych to złożone zadanie, które wymaga czasu, systematycznego podejścia i staranności w każdym z etapów. Eksploracyjna analiza danych (EDA) jest jednym z fundamentalnych kroków tego procesu.
W niniejszym artykule przybliżymy koncepcję eksploracyjnej analizy danych, a także pokażemy, jak można ją zrealizować za pomocą języka R.
Czym jest eksploracyjna analiza danych?
Eksploracyjna analiza danych to proces badania i charakteryzowania zbioru danych przed jego wykorzystaniem w konkretnej aplikacji – czy to biznesowej, statystycznej, czy też w ramach uczenia maszynowego.
Podsumowanie informacji oraz jej podstawowych cech odbywa się zazwyczaj za pomocą metod wizualnych, takich jak wykresy, tabele i histogramy. Praktyka ta jest stosowana w celu oceny potencjału danych przed poddaniem ich bardziej zaawansowanym procedurom.
W związku z tym EDA umożliwia:
- Formułowanie hipotez odnośnie wykorzystania danych;
- Odkrywanie ukrytych szczegółów w strukturze danych;
- Identyfikowanie brakujących wartości, odchyleń lub nieprawidłowych wzorców;
- Wykrywanie trendów i kluczowych zależności;
- Odrzucenie zmiennych nieistotnych lub silnie skorelowanych z innymi;
- Określenie właściwego podejścia do modelowania formalnego.
Różnica między analizą opisową a eksploracyjną
Analiza danych dzieli się na dwa główne nurty: opisową i eksploracyjną, które wzajemnie się uzupełniają, choć ich cele są różne.
Analiza opisowa koncentruje się na przedstawieniu charakterystyki zmiennych, np. poprzez obliczenie średniej, mediany czy dominanty.
Natomiast analiza eksploracyjna dąży do zidentyfikowania zależności między zmiennymi, wyciągnięcia wstępnych wniosków i nakierowania modelowania w kontekście uczenia maszynowego: klasyfikacji, regresji i grupowania.
Obydwa rodzaje analizy mogą wykorzystywać graficzne reprezentacje danych. Jednak tylko analiza eksploracyjna ma na celu dostarczenie praktycznych wniosków, które prowokują decydentów do podjęcia działań.
Podsumowując, eksploracyjna analiza danych koncentruje się na rozwiązywaniu problemów i dostarczaniu rozwiązań, które ukierunkują dalsze etapy modelowania, natomiast analiza opisowa służy wyłącznie do przedstawienia szczegółowego opisu danego zbioru danych.
Analiza opisowa | Eksploracyjna analiza danych
Analizuje zachowanie | Analizuje zachowanie i relacje
Zapewnia podsumowanie | Prowadzi do specyfikacji i działań
Organizuje dane w tabelach i na wykresach | Porządkuje dane w tabelach i na wykresach
Nie ma znaczącej mocy wyjaśniającej | Ma znaczącą moc wyjaśniającą
Praktyczne zastosowania EDA
1. Marketing cyfrowy
Marketing cyfrowy ewoluował od podejścia kreatywnego do procesu opartego na danych. Działy marketingu wykorzystują eksploracyjną analizę danych do oceny skuteczności kampanii i działań, a także do podejmowania decyzji inwestycyjnych i kierowania komunikacji do konsumentów.
Badania demograficzne, segmentacja klientów oraz inne techniki pozwalają marketerom analizować obszerne dane dotyczące zachowań zakupowych konsumentów, ankiet i paneli, co pozwala lepiej zrozumieć i dostosować strategię marketingową.
Analiza eksploracyjna aktywności w sieci umożliwia marketerom gromadzenie informacji o interakcjach użytkowników na stronie internetowej na poziomie sesji. Google Analytics jest przykładem popularnego i darmowego narzędzia analitycznego, które służy do tego celu.
W marketingu często stosuje się techniki eksploracyjne takie jak modelowanie mixu marketingowego, analizę cen i promocji, optymalizację sprzedaży oraz eksploracyjną analizę klientów, np. w celu segmentacji.
2. Analiza portfela
Popularnym zastosowaniem eksploracyjnej analizy danych jest analiza portfelowa. Bank lub instytucja pożyczkowa dysponuje zbiorem rachunków o różnej wartości i poziomie ryzyka.
Rachunki mogą różnić się w zależności od statusu społecznego posiadacza (np. zamożny, klasa średnia, uboższy), położenia geograficznego, majątku i wielu innych czynników. Pożyczkodawca musi znaleźć równowagę między zwrotem z pożyczki a ryzykiem niewypłacalności. Pojawia się więc pytanie, jak ocenić wartość całego portfela.
Pożyczki o najniższym poziomie ryzyka mogą być przyznawane osobom zamożnym, ale ich liczba jest ograniczona. Z drugiej strony, wiele osób o niższych dochodach może pożyczać, ale wiąże się to z większym ryzykiem.
Dzięki eksploracyjnej analizie danych można połączyć analizę szeregów czasowych z innymi czynnikami, aby podjąć decyzję, kiedy i na jakich warunkach udzielać pożyczek różnym grupom pożyczkobiorców. Odsetki naliczane członkom portfela służą do pokrycia strat wynikających z niewypłacalności w danym segmencie.
3. Analiza ryzyka
Modele predykcyjne stosowane w bankowości służą do oceny ryzyka związanego z konkretnymi klientami. Oceny zdolności kredytowej, oparte na prognozie zachowań w przeszłości, są powszechnie używane do oceny wiarygodności każdego wnioskodawcy.
Analiza ryzyka jest również stosowana w nauce i branży ubezpieczeniowej. Jest także ważna dla instytucji finansowych, np. firm obsługujących płatności online, w celu weryfikacji autentyczności transakcji.
W tym celu analizowana jest historia transakcji klienta. Często ma to miejsce przy płatnościach kartą kredytową – w przypadku nagłego wzrostu liczby transakcji klient otrzymuje telefon z prośbą o potwierdzenie operacji. Pomaga to w minimalizacji strat finansowych.
Eksploracyjna analiza danych w R
Aby rozpocząć eksploracyjną analizę danych w R, należy zainstalować i uruchomić podstawową wersję R oraz R Studio (IDE), a następnie załadować i zainstalować pakiety:
#Instalowanie pakietów
install.packages("dplyr")
install.packages("ggplot2")
install.packages("magrittr")
install.packages("tsibble")
install.packages("forecast")
install.packages("skimr")
#Ładowanie pakietów
library(dplyr)
library(ggplot2)
library(magrittr)
library(tsibble)
library(forecast)
library(skimr)
W tym samouczku wykorzystamy wbudowany w R zbiór danych ekonomicznych, zawierający roczne wskaźniki gospodarcze dla USA. Dla uproszczenia zmienimy jego nazwę na „econ”:
econ <- ggplot2::economics
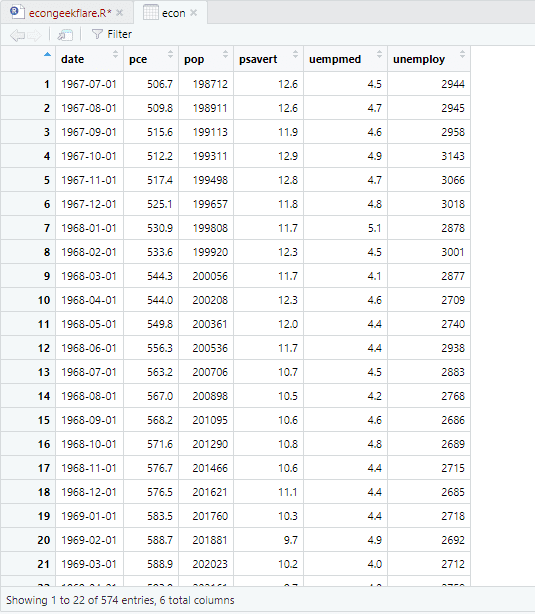
Do przeprowadzenia analizy opisowej wykorzystamy pakiet „skimr”, który w przejrzysty sposób wylicza statystyki:
#Analiza opisowa skimr::skim(econ)
Możemy także użyć funkcji „summary”:
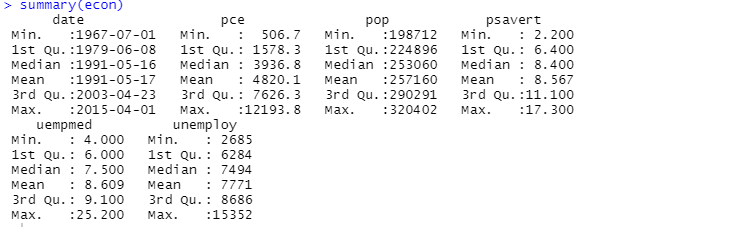
Analiza opisowa pokazuje, że zbiór danych „econ” zawiera 547 wierszy i 6 kolumn. Najwcześniejsza data to 1967-07-01, a najpóźniejsza to 2015-04-01. Podane są także średnie i odchylenia standardowe.
Mamy już podstawowy pogląd na zbiór danych „econ”. Stwórzmy histogram, aby przyjrzeć się bliżej rozkładowi danych:
#Histogram bezrobocia econ %>% ggplot2::ggplot() + ggplot2::aes(x = uempmed) + ggplot2::geom_histogram() + labs(x = "Bezrobocie", title = "Miesięczne bezrobocie w USA w latach 1967-2015")
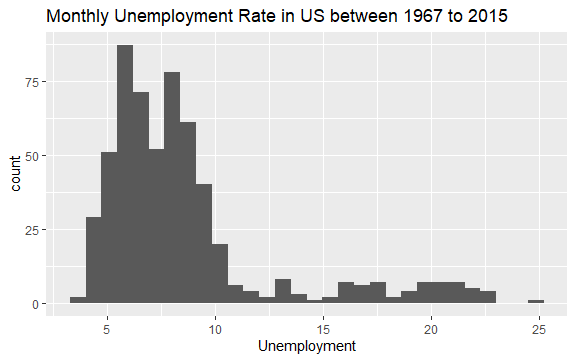
Rozkład histogramu wskazuje na wydłużony prawy ogon, co sugeruje obecność obserwacji o bardziej skrajnych wartościach. Pojawia się pytanie: w jakim okresie te wartości wystąpiły i jaki jest trend zmiennej?
Najprostszym sposobem identyfikacji trendu jest wykres liniowy. Poniżej generujemy wykres liniowy z dodaną linią wygładzającą:
#Wykres liniowy bezrobocia econ %>% ggplot2::autoplot(uempmed) + ggplot2::geom_smooth()
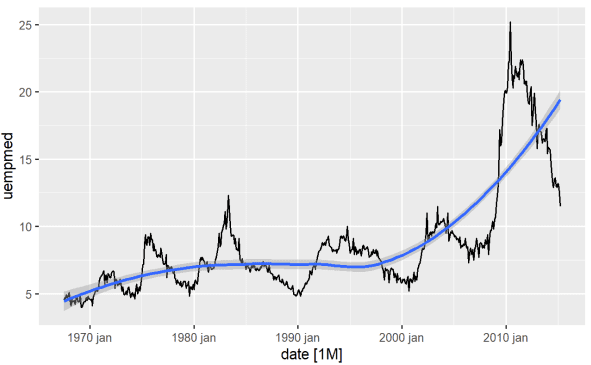
Z wykresu wynika, że w okolicach roku 2010 bezrobocie wzrosło, przekraczając wartości obserwowane w poprzednich dekadach.
Istotną kwestią, zwłaszcza w modelowaniu ekonometrycznym, jest stacjonarność szeregu czasowego, czyli stałość średniej i wariancji w czasie.
Gdy założenia te nie są spełnione, mamy do czynienia z szeregiem niestacjonarnym, gdzie szoki powodują trwały efekt.
Wydaje się, że tak jest w przypadku czasu pozostawania bez pracy. Obserwujemy znaczące wahania, co ma wpływ na teorie ekonomiczne dotyczące cykli. Jak praktycznie sprawdzić, czy zmienna jest stacjonarna?
Pakiet „forecast” posiada funkcję do przeprowadzania testów stacjonarności, takich jak ADF, KPSS, która zwraca liczbę różnic potrzebnych do osiągnięcia stacjonarności:
#Test ADF weryfikujący stacjonarność forecast::ndiffs( x = econ$uempmed, test = "adf")
Wartość p większa niż 0.05 wskazuje, że dane nie są stacjonarne.
Inną ważną kwestią jest identyfikacja korelacji pomiędzy opóźnionymi wartościami szeregu czasowego. Pomocne są w tym korelogramy ACF i PACF.
Ponieważ szereg nie ma sezonowości, a jedynie trend, autokorelacje na początku są zwykle duże i dodatnie, gdyż obserwacje bliskie w czasie są podobne.
Funkcja autokorelacji (ACF) dla szeregów z trendem zazwyczaj przyjmuje wartości dodatnie, które powoli maleją wraz ze wzrostem opóźnienia.
#Reszty bezrobocia checkresiduals(econ$uempmed) pacf(econ$uempmed)
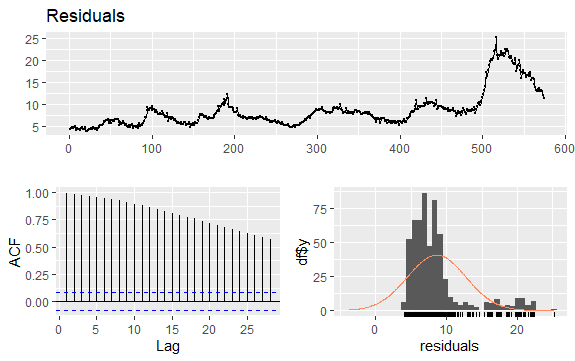
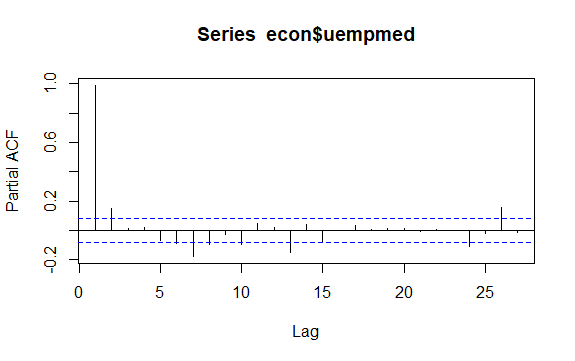
Podsumowanie
Po otrzymaniu danych, które są w miarę uporządkowane, pojawia się chęć, aby od razu przejść do budowy modelu. Warto jednak powstrzymać się od tej pokusy i zacząć od eksploracyjnej analizy danych, która jest prosta, a zarazem pozwala uzyskać cenne informacje.
Zachęcamy również do zapoznania się z dodatkowymi materiałami na temat statystyki w nauce o danych.
newsblog.pl