3 sposoby mnożenia macierzy w Pythonie

Mnożenie Macierzy w Pythonie: Kompletny Przewodnik

Ten poradnik przedstawi Ci krok po kroku, jak efektywnie mnożyć macierze w języku Python. Rozpoczniemy od omówienia zasad, które decydują o poprawności mnożenia macierzy, a następnie stworzymy własną funkcję w Pythonie, która to zadanie zrealizuje. Następnie, zapoznasz się z możliwością osiągnięcia identycznego rezultatu, wykorzystując zagnieżdżone konstrukcje listowe. Na koniec, wykorzystamy bibliotekę NumPy z jej wbudowanymi narzędziami, aby w sposób optymalny pomnażać macierze.

Kiedy Mnożenie Macierzy Jest Wykonalne?

Zanim przejdziemy do implementacji kodu w Pythonie, warto zrozumieć fundamentalne zasady mnożenia macierzy.

Mnożenie dwóch macierzy, oznaczonych jako A i B, jest możliwe tylko wtedy, gdy liczba kolumn macierzy A jest identyczna z liczbą wierszy macierzy B.

Być może spotkałeś się już z tym warunkiem. Czy zastanawiałeś się jednak, skąd on wynika?

Wynika to z mechanizmu działania mnożenia macierzy. Spójrz na poniższą ilustrację.

W naszym ogólnym przykładzie macierz A składa się z m wierszy i n kolumn, natomiast macierz B ma n wierszy i p kolumn.

Jaki Kształt Ma Macierz Wynikowa?

Element o indeksie (i, j) w macierzy wynikowej C powstaje poprzez obliczenie iloczynu skalarnego i-tego wiersza macierzy A oraz j-tej kolumny macierzy B.

A zatem, aby otrzymać element o konkretnym indeksie w macierzy wynikowej C, należy obliczyć iloczyn skalarny odpowiedniego wiersza i kolumny z macierzy A i B.

Powtarzając ten proces, otrzymamy macierz wynikową C o wymiarach mxp, czyli z m wierszami i p kolumnami, co pokazano poniżej.

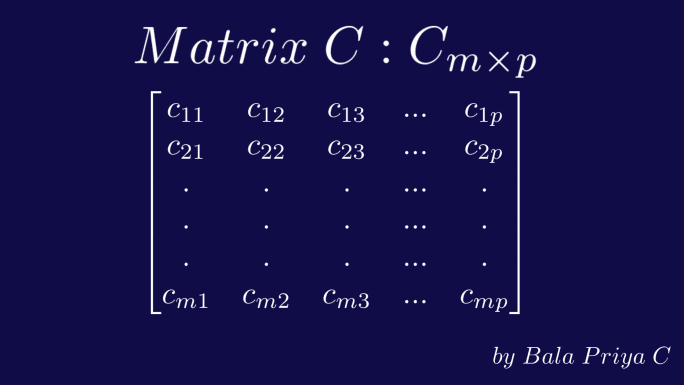
Iloczyn skalarny dwóch wektorów a i b definiuje się następującym wzorem:

Podsumowując:

• Iloczyn skalarny można obliczyć tylko dla wektorów o jednakowej długości.
• Aby iloczyn skalarny wiersza i kolumny podczas mnożenia macierzy był prawidłowy, oba muszą mieć identyczną liczbę elementów.
• W naszym przykładzie ogólnym każdy wiersz macierzy A zawiera n elementów, a każda kolumna macierzy B również n elementów.

Z powyższego wynika, że liczba kolumn macierzy A musi być taka sama jak liczba wierszy macierzy B. To właśnie tłumaczy ten warunek.

Mam nadzieję, że teraz rozumiesz, kiedy mnożenie macierzy jest poprawne i jak uzyskuje się elementy macierzy wynikowej.

Przejdźmy teraz do pisania kodu w Pythonie, który wykona mnożenie dwóch macierzy.

Implementacja Własnej Funkcji Mnożenia Macierzy

Zacznijmy od napisania funkcji, która będzie mnożyć macierze.

Ta funkcja powinna:

• Przyjmować dwie macierze, A i B, jako dane wejściowe.
• Sprawdzać, czy mnożenie macierzy A i B jest poprawne.
• W przypadku poprawności, mnożyć macierze A i B i zwracać macierz wynikową C.
• W przeciwnym razie, zwracać informację o błędzie, że macierze A i B nie mogą być pomnożone.

Krok 1: Wygenerujmy dwie macierze liczb całkowitych, wykorzystując funkcję random.randint() biblioteki NumPy. Możemy też zdefiniować macierze jako zagnieżdżone listy w Pythonie.

import numpy as np
np.random.seed(27)
A = np.random.randint(1,10,size = (3,3))
B = np.random.randint(1,10,size = (3,2))
print(f"Macierz A:n {A}n")
print(f"Macierz B:n {B}n")
# Wynik
Macierz A:
 [[4 9 9]
 [9 1 6]
 [9 2 3]]
Macierz B:
 [[2 2]
 [5 7]
 [4 4]]
    

Krok 2: Zdefiniujmy funkcję `multiply_matrix(A,B)`. Funkcja ta przyjmuje dwie macierze A i B i zwraca macierz wynikową C, o ile mnożenie macierzy jest poprawne.

def multiply_matrix(A,B):
  global C
  if  A.shape[1] == B.shape[0]:
    C = np.zeros((A.shape[0],B.shape[1]),dtype = int)
    for row in range(len(A)):
        for col in range(len(B[0])):
            for elt in range(len(B)):
              C[row, col] += A[row, elt] * B[elt, col]
    return C
  else:
    return "Nie można pomnożyć macierzy A i B."

Analiza Definicji Funkcji

Przeanalizujmy teraz definicję naszej funkcji.

Zadeklaruj zmienną C jako globalną: W Pythonie zmienne deklarowane wewnątrz funkcji mają zasięg lokalny i nie są dostępne spoza funkcji. Aby macierz wynikowa C była dostępna, musimy zadeklarować ją jako zmienną globalną. W tym celu używamy słowa kluczowego `global` przed nazwą zmiennej.

Sprawdzenie poprawności mnożenia macierzy: Za pomocą atrybutu `shape` sprawdzamy, czy macierze A i B mogą być pomnożone. Dla tablicy `arr`, `arr.shape[0]` i `arr.shape[1]` zwracają odpowiednio liczbę wierszy i kolumn. Warunek `A.shape[1] == B.shape[0]` sprawdza, czy mnożenie jest wykonalne. Jeśli warunek jest spełniony, wyliczana jest macierz wynikowa. W przeciwnym wypadku zwracany jest komunikat błędu.

Pętle zagnieżdżone do obliczenia wartości: Do wyliczenia elementów macierzy wynikowej, musimy iterować przez wiersze macierzy A (zewnętrzna pętla `for`). Wewnętrzna pętla `for` iteruje przez kolumny macierzy B. Najbardziej wewnętrzna pętla `for` pomaga nam dostać się do poszczególnych elementów kolumny.

▶️ Po zrozumieniu działania funkcji mnożenia macierzy, wywołajmy ją, używając macierzy A i B, które wcześniej wygenerowaliśmy.

multiply_matrix(A,B)
# Wynik
array([[ 89, 107],
       [ 47,  49],
       [ 40,  44]])
    

Ponieważ mnożenie macierzy A i B jest prawidłowe, funkcja `multiply_matrix()` zwraca macierz wynikową C.

Mnożenie Macierzy z Użyciem Zagnieżdżonej Listy Składanej

W poprzednim rozdziale utworzyliśmy własną funkcję do mnożenia macierzy. Teraz, zobaczysz jak można osiągnąć ten sam efekt przy użyciu zagnieżdżonej list składanej.

Poniżej znajduje się zagnieżdżona lista składana do mnożenia macierzy.

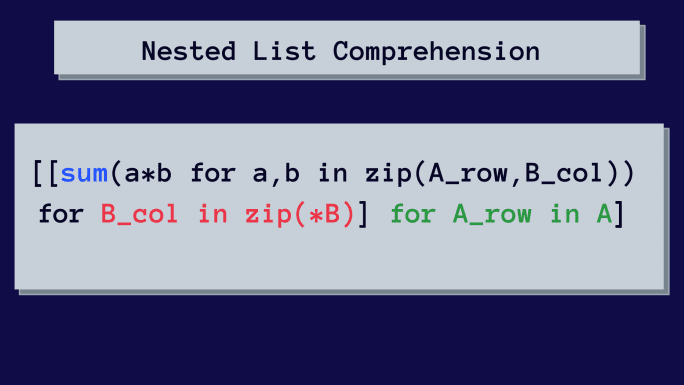
Na pierwszy rzut oka może wydawać się to skomplikowane. Dokładnie przeanalizujemy tę zagnieżdżoną listę, krok po kroku.

Skupmy się na jednym elemencie listy składanej, aby zrozumieć, co robi.

Użyjemy następującego ogólnego szablonu do analizy list składanych:

[<wykonaj-to> for <element> in <iterowalny-obiekt>]
gdzie:
<wykonaj-to>: operacja lub wyrażenie, które chcesz wykonać
<element>:  element, dla którego operacja ma zostać wykonana
<iterowalny-obiekt>: iterowalny obiekt (lista, krotka, itp.), po którym iterujemy
    

▶️ Zachęcam do zapoznania się z naszym przewodnikiem: List Comprehension w Pythonie – z przykładami, aby uzyskać pełne zrozumienie tej techniki.

Zanim pójdziemy dalej, pamiętajmy, że celem jest skonstruowanie macierzy wynikowej C, wiersz po wierszu.

Analiza Zagnieżdżonej Listy Składanej

Krok 1: Wyliczenie pojedynczej wartości macierzy C

Dla danego wiersza `i` macierzy A i kolumny `j` macierzy B, poniższe wyrażenie daje element o indeksie (i, j) macierzy C.

sum(a*b for a,b in zip(A_row, B_col))
# zip(A_row, B_col) zwraca iterator krotek
# Jeśli A_row = [a1, a2, a3] & B_col = [b1, b2, b3]
# zip(A_row, B_col) zwróci (a1, b1), (a2, b2), itd.
    

Jeśli `i` = `j` = 1, wyrażenie zwróci element c_11 macierzy C. W ten sposób można uzyskać jeden element w jednym wierszu.

Krok 2: Konstrukcja pojedynczego wiersza macierzy C

Następnie, celem jest zbudowanie całego wiersza.

Dla pierwszego wiersza macierzy A, należy przeiterować przez wszystkie kolumny macierzy B, aby otrzymać pełny wiersz macierzy C.

Wróćmy do szablonu listy składanej:

• Zastąp `<wykonaj-to>` wyrażeniem z kroku 1, ponieważ to chcemy osiągnąć.
• Zastąp `<element>` przez `B_col` – każda kolumna macierzy B.
• Zastąp `<iterowalny-obiekt>` przez `zip(*B)` – lista zawierająca wszystkie kolumny macierzy B.

A oto nasza pierwsza lista składana:

[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
# zip(*B): * to operator rozpakowania
# zip(*B) zwraca listę kolumn macierzy B
    

Krok 3: Konstrukcja wszystkich wierszy i otrzymanie macierzy C

Teraz musimy wypełnić macierz wynikową C, obliczając pozostałe wiersze. W tym celu musimy przejść przez wszystkie wiersze macierzy A.

Wróćmy raz jeszcze do listy składanej:

• Zastąp `<wykonaj-to>` listą z kroku 2, gdzie obliczyliśmy cały wiersz.
• Zastąp `<element>` przez `A_row` – każdy wiersz macierzy A.
• `<iterowalny-obiekt>` to macierz A, po której iterujemy wierszami.

Oto nasza ostateczna, zagnieżdżona lista składana.🎉

[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
  for A_row in A]
    

Czas zweryfikować wynik! ✔

# konwertujemy na tablicę NumPy za pomocą np.array()
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
  for A_row in A])

# Wynik:
[[ 89 107]
 [ 47  49]
 [ 40  44]]
    

Widać, że jest to odpowiednik zagnieżdżonych pętli `for`, z tą różnicą, że jest to bardziej zwarta forma.

Można to zrobić jeszcze bardziej wydajnie, korzystając z wbudowanych funkcji. Przejdźmy do następnej sekcji.

Mnożenie Macierzy z Użyciem NumPy `matmul()`

Funkcja `np.matmul()` przyjmuje dwie macierze i zwraca ich iloczyn, o ile mnożenie jest prawidłowe.

C = np.matmul(A,B)
print(C)
# Wynik:
[[ 89 107]
 [ 47  49]
 [ 40  44]]
    

Widać, że ta metoda jest prostsza, niż dwie poprzednie. Zamiast `np.matmul()` można użyć operatora `@`, co pokażemy za chwilę.

Użycie Operatora `@` do Mnożenia Macierzy

Operator `@` w Pythonie, służy do wykonywania mnożenia macierzy.

Działa na dwóch macierzach (a ogólnie na tablicach N-wymiarowych NumPy) i zwraca macierz wynikową.

Uwaga: Aby używać operatora `@`, musisz mieć Pythona w wersji 3.5 lub nowszej.

Oto jak go używać:

C = A @ B
print(C)
# Wynik
array([[ 89, 107],
       [ 47,  49],
       [ 40,  44]])
    

Macierz wynikowa C jest identyczna z tą, którą uzyskaliśmy wcześniej.

Czy Można Użyć `np.dot()` do Mnożenia Macierzy?

Jeśli spotkałeś się z kodem, który używa `np.dot()` do mnożenia macierzy, oto jak to działa.

C = np.dot(A,B)
print(C)
# Wynik:
[[ 89 107]
 [ 47  49]
 [ 40  44]]
    

Jak widać, `np.dot(A, B)` również zwraca oczekiwaną macierz wynikową.

Jednak, jak wynika z dokumentacji NumPy, `np.dot()` powinno się używać wyłącznie do obliczania iloczynu skalarnego dwóch wektorów jednowymiarowych, a nie do mnożenia macierzy.

Pamiętajmy, że element o indeksie (i, j) macierzy wynikowej C jest iloczynem skalarnym i-tego wiersza macierzy A i j-tej kolumny macierzy B.

NumPy rozgłasza w sposób automatyczny operację iloczynu skalarnego do wszystkich wierszy i kolumn, dzięki czemu otrzymujemy macierz wynikową. Jednak, w trosce o czytelność i unikanie niejednoznaczności, należy używać `np.matmul()` lub operatora `@`.

Podsumowanie

🎯 W tym tutorialu nauczyliśmy się:

• Warunku poprawnego mnożenia macierzy: liczba kolumn macierzy A musi być równa liczbie wierszy macierzy B.
• Jak napisać własną funkcję w Pythonie, która sprawdza, czy mnożenie jest możliwe i zwraca macierz wynikową (funkcja opiera się na zagnieżdżonych pętlach `for`).
• Używania zagnieżdżonych list składanych do mnożenia macierzy – są one bardziej zwięzłe niż pętle `for`, ale mniej czytelne.
• Wykorzystywania wbudowanej funkcji NumPy `np.matmul()` do mnożenia macierzy, co jest najwydajniejszą metodą.
• Operatora `@` do mnożenia dwóch macierzy w Pythonie.

Na tym kończymy omówienie mnożenia macierzy w Pythonie. Następnie możesz nauczyć się, jak sprawdzić, czy liczba jest pierwsza, lub rozwiązywać interesujące problemy związane z łańcuchami znaków.

Powodzenia w nauce! 🎉