W świecie analizy danych, zarówno w sektorze prywatnym, jak i publicznym, testowanie hipotez stanowi fundamentalne narzędzie. Umożliwia ono formułowanie i weryfikację przypuszczeń dotyczących charakterystyki populacji na podstawie danych z próby.
Osoby pracujące z danymi populacyjnymi lub zgłębiające tę tematykę z pewnością zetknęły się z testowaniem hipotez – niezwykle przydatną metodą analityczną.
Istnieje wiele metod formułowania założeń, lecz nie każda z nich gwarantuje wysoki stopień precyzji.
Bazowanie na niepewnych danych może generować ryzyko dla organizacji, dlatego tak istotne jest wykorzystywanie solidnych metod badawczych.
Testowanie hipotez jest strategią pozwalającą na osiągnięcie większej dokładności analiz i odgrywa kluczową rolę w badaniu charakterystyki populacji.
W dalszej części artykułu przybliżymy, czym dokładnie jest testowanie hipotez, jak funkcjonuje, jakie korzyści niesie jego stosowanie oraz gdzie znajduje praktyczne zastosowanie.
Przejdźmy zatem do sedna sprawy!
Czym jest testowanie hipotez?
Testowanie hipotez to metoda statystycznego wnioskowania, która umożliwia analitykom weryfikację, czy posiadane dane z próby dostatecznie potwierdzają daną hipotezę, pozwalając na formułowanie wniosków o całej populacji.
Dzięki tej technice analitycy mogą rzetelnie ocenić postawioną hipotezę i określić poziom jej prawdziwości w oparciu o zgromadzone dane.
Mówiąc wprost, jest to proces oparty na statystyce, który pozwala na wyciągnięcie wniosków dotyczących populacji na podstawie analizy danych z próby.
Zazwyczaj bezpośrednie zbadanie wszystkich właściwości lub parametrów całej populacji jest niemożliwe. Jednak testowanie hipotez umożliwia tworzenie uzasadnionych prognoz i podejmowanie decyzji na podstawie analizy danych z próby i ich dokładności.
Rodzaje hipotez w testowaniu
Wyróżniamy następujące rodzaje hipotez:
- Hipoteza zerowa: Zakłada, że dane z próby są przypadkowe i nie wykazują żadnej korelacji między badanymi zmiennymi.
- Hipoteza alternatywna: Prezentuje tezę przeciwną do hipotezy zerowej i stanowi główny cel testowania. Sugeruje istnienie związku pomiędzy zmiennymi w próbie.
- Hipoteza niekierunkowa: Zakłada brak konkretnego kierunku zależności między zmiennymi w próbie. Jest to hipoteza dwustronna, która stwierdza, że prawdziwa wartość nie jest identyczna z wartością przewidywaną.
- Hipoteza kierunkowa: Określa konkretny rodzaj związku między zmiennymi. Sugeruje, że jedna zmienna w próbie może wpływać na inną w określony sposób.
- Hipoteza statystyczna: Ułatwia analitykom ocenę, czy dane i ich wartości spełniają założenia danej hipotezy. Jest niezwykle przydatna w formułowaniu twierdzeń i prognoz dotyczących parametrów populacji na podstawie danych z próby.
Teraz przejdziemy do omówienia metod wykorzystywanych w testowaniu hipotez.
Metody testowania hipotez
Aby ocenić prawdziwość hipotezy, analityk musi zgromadzić wiarygodne dowody, na podstawie których można wyciągnąć wnioski. W procesie testowania, jeszcze przed jego rozpoczęciem, ustala się hipotezę zerową oraz hipotezę alternatywną.
Testowanie hipotez wykorzystuje różnorodne metody w celu oceny przydatności danych z próby. Wybór odpowiedniej metody zależy od charakterystyki danych oraz wielkości próby.
Testowanie normalności
Jest to standardowa metoda stosowana do oceny, czy dane z próby mają rozkład normalny. W trakcie testu sprawdza się, czy punkty danych skupione wokół średniej rozkładają się równomiernie, czy też wykazują odchylenia.
W tym teście statystycznym prawdopodobieństwo, że punkty danych przekroczą lub znajdą się poniżej średniej, jest zbliżone. Efektem jest utworzenie krzywej dzwonowej, symetrycznie rozłożonej wokół średniej.
Test Z
Test Z stosuje się, gdy populacja ma rozkład normalny. Służy do weryfikacji, czy średnie dwóch odrębnych populacji są różne, w sytuacji, gdy znana jest wariancja danych.
Ten typ testu jest często wykorzystywany przy analizie danych populacji, gdy wielkość próby przekracza trzydzieści. Zgodnie z centralnym twierdzeniem granicznym, w miarę wzrostu liczebności próby, rozkład próby dąży do rozkładu normalnego, co uzasadnia stosowanie testu Z.
Test T-Studenta
Test t-Studenta jest wykorzystywany, gdy wielkość próby jest ograniczona i zwykle ma rozkład zbliżony do normalnego. Jest szczególnie przydatny, gdy wielkość próby jest mniejsza niż 30 i nie znamy odchylenia standardowego populacji.
Wykonując test t, oblicza się przedziały ufności dla określonych danych populacji.
Test chi-kwadrat
Test chi-kwadrat to popularna metoda testowania hipotez, która służy do oceny dopasowania i zgodności rozkładu danych.
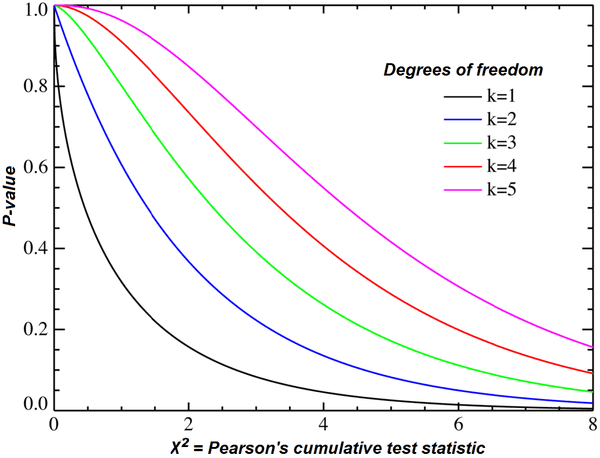 Źródło: wikipedia.org
Źródło: wikipedia.org
Jednak najczęstszym zastosowaniem tego testu jest weryfikacja wariancji populacji w odniesieniu do wariancji populacji o znanej lub zakładanej wartości. Wyróżniamy różne rodzaje testów chi-kwadrat, najczęściej wykorzystywane to test wariancji i test niezależności chi-kwadrat.
Test ANOVA

Analiza wariancji (ANOVA) jest statystyczną metodą testowania, która pozwala porównywać zestawy danych z dwóch lub więcej próbek, a w szczególności umożliwia porównanie więcej niż dwóch średnich jednocześnie.
Umożliwia także analizę zmiennej zależnej i niezależnej w danych z próby. Test ANOVA jest podobny w zastosowaniu do testów Z i T, ale te dwa ostatnie ograniczone są do porównywania jedynie dwóch średnich.
Jak działa testowanie hipotez?
Analiza danych w procesie testowania hipotez opiera się na losowo dobranych próbach. Zebrane dane wykorzystuje się do zweryfikowania hipotezy zerowej oraz alternatywnej.
Jak wspomniano wcześniej, hipoteza zerowa i alternatywna wykluczają się wzajemnie i tylko jedna z nich może być prawdziwa w procesie testowania.
Należy jednak pamiętać, że odrzucenie hipotezy zerowej nie zawsze oznacza, że hipoteza alternatywna jest prawdziwa.
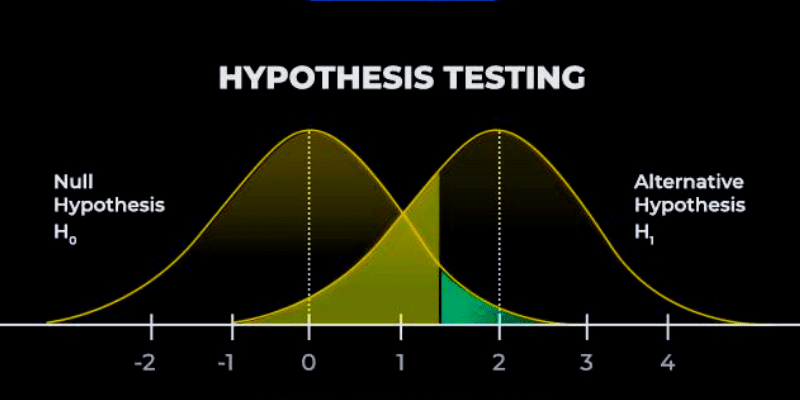 Źródło: kroki analityczne
Źródło: kroki analityczne
Wartość p: Podczas procesu testowania ważną rolę odgrywa wartość p, inaczej wartość prawdopodobieństwa. Określa ona istotność wyniku. Wartość p wskazuje także na ryzyko popełnienia błędu podczas odrzucenia lub nieodrzucenia hipotezy zerowej. Wartość p przyjmuje wartości od 0 do 1, które następnie porównuje się z poziomem istotności (alfa).
Poziom istotności określa akceptowalny poziom ryzyka odrzucenia hipotezy zerowej w trakcie testowania. Należy mieć świadomość, że w procesie testowania hipotez mogą wystąpić dwa rodzaje błędów:
- Błąd pierwszego rodzaju (błąd alfa) pojawia się, gdy test odrzuca hipotezę zerową, która w rzeczywistości jest prawdziwa.
- Błąd drugiego rodzaju (błąd beta) występuje, gdy test akceptuje hipotezę zerową, która w rzeczywistości jest fałszywa.
Wszystkie wartości, które prowadzą do odrzucenia hipotezy zerowej, znajdują się w tak zwanym obszarze krytycznym. Wartość krytyczna oddziela obszar krytyczny od pozostałych.
Kroki w procesie testowania hipotez
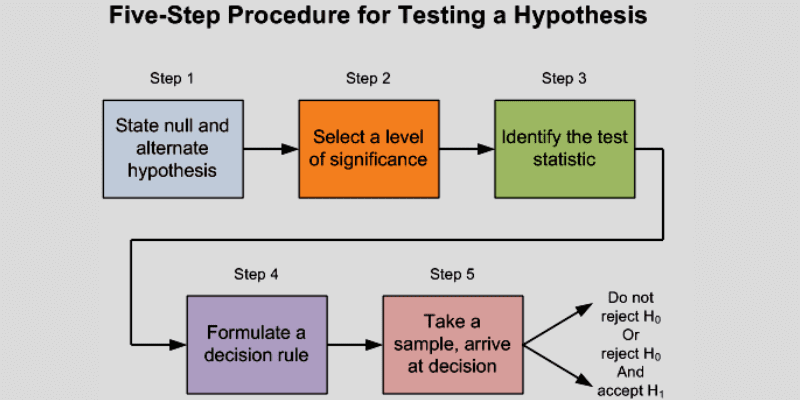 źródło: medium
źródło: medium
Proces testowania hipotez składa się z czterech głównych etapów:
- Sformułowanie hipotez: Na początku należy zdefiniować dwie hipotezy, przy czym tylko jedna z nich może być prawdziwa. Hipoteza zerowa może stwierdzać, że nie ma różnicy w średnim wskaźniku BMI, natomiast hipoteza alternatywna zakłada istnienie znaczącej różnicy.
- Planowanie: Następnym krokiem jest opracowanie planu analizy danych z próby. Niezwykle istotne jest przeprowadzenie odpowiedniego próbkowania i zebranie reprezentatywnych danych.
- Analiza danych z próby: Po określeniu sposobu oceny danych, należy przejść do ich analizy, aby uniknąć nadmiarowości. Podczas analizy należy upewnić się, że próby są od siebie niezależne i wystarczająco duże.
- Obliczenie statystyk testu: Na tym etapie oblicza się statystyki testu i wyznacza wartość p, przy założeniu, że hipoteza zerowa jest prawdziwa.
- Ocena wyniku: Na końcu analizuje się wynik testu hipotezy i decyduje o odrzuceniu lub przyjęciu hipotezy zerowej, opierając się na danych z próby.
Przejdźmy teraz do omówienia korzyści płynących z testowania hipotez.
Korzyści wynikające z testowania hipotez
Główne zalety stosowania testowania hipotez to:
- Pozwala ocenić zasadność wniosków i decyzji na podstawie danych.
- Tworzy wiarygodne środowisko dla podejmowania decyzji w oparciu o dane z próby.
- Umożliwia ocenę, czy dane z próby wykorzystane w testowaniu hipotez są statystycznie istotne.
- Zwiększa wiarygodność i trafność wyników testów w każdym systematycznym procesie badawczym.
Ułatwia ekstrapolację danych z próby na większą populację, w zależności od potrzeb.
Zastosowania testowania hipotez
Testowanie hipotez znajduje zastosowanie w wielu branżach, umożliwiając rzetelną ocenę dokładności danych z próby. Poniżej przedstawiamy kilka przykładów:
#1. Badania kliniczne
W badaniach klinicznych testowanie hipotez odgrywa istotną rolę, ponieważ umożliwia lekarzom ocenę skuteczności nowych leków, metod leczenia lub procedur na podstawie danych z próby.
Przykładowo, lekarz może przypuszczać, że nowe leczenie obniży poziom potasu u pacjentów. W tym celu może zmierzyć poziom potasu przed i po zastosowaniu kuracji.

Lekarz formułuje hipotezy: H0: Upo = Uprzed, czyli poziom potasu po kuracji jest taki sam jak przed nią, oraz Ha: Upo < Uprzed, czyli poziom potasu obniżył się po zastosowaniu kuracji.
W przypadku, gdy wartość p jest niższa niż poziom istotności, lekarz może stwierdzić, że leczenie obniża poziom potasu.
#2. Produkcja
W przemyśle produkcyjnym testowanie hipotez pomaga menedżerom ocenić, czy nowa metoda lub technologia jest skuteczna.
Na przykład, firma produkcyjna może wykorzystać testowanie hipotez, aby sprawdzić, czy nowa metoda pomaga zredukować liczbę wadliwych produktów na partię. Załóżmy, że dotychczasowa liczba wadliwych produktów wynosiła 300 na partię.

Producent porównuje średnią liczbę wadliwych produktów wyprodukowanych przed i po wprowadzeniu nowej metody. Formułowane są hipotezy: H0: Upo = Uprzed, co oznacza, że średnia liczba wadliwych produktów po zmianie metody jest taka sama, oraz HA: Upo ≠ Uprzed, co oznacza, że liczba wadliwych produktów uległa zmianie.
Po przeprowadzeniu testu i stwierdzeniu, że wartość p jest mniejsza niż poziom istotności, firma produkcyjna może wywnioskować, że liczba wadliwych produktów uległa zmianie.
#3. Rolnictwo
Testowanie hipotez jest często wykorzystywane w rolnictwie do analizy wpływu nawozów lub pestycydów na wzrost i odporność roślin. Na przykład, biolodzy mogą wykorzystać testy, aby sprawdzić, czy dany nawóz zwiększy wzrost rośliny o więcej niż 15 cali.

Biolodzy mogą obserwować roślinę pod wpływem nawozu przez określony czas, a następnie zebrać dane. W trakcie testu hipotezą zerową jest H0: U=15 cali, co sugeruje, że nawóz nie wpływa na średni wzrost rośliny. Alternatywna hipoteza to HA: U> 15 cali, co oznacza, że nawóz zwiększa średni wzrost rośliny. Jeśli po przeprowadzeniu testu wartość p jest mniejsza niż poziom istotności, biolog może potwierdzić, że nawóz zwiększa wzrost rośliny.
Zasoby edukacyjne
#1. Statystyka: wprowadzenie krok po kroku od Udemy

Udemy oferuje kurs z zakresu statystyki, który obejmuje krok po kroku wprowadzenie do statystyki, w tym testowanie hipotez. Kurs ten zawiera przykłady i lekcje od byłego analityka danych Google, które pozwolą Ci na opanowanie tematów takich jak przedziały ufności i testowanie hipotez.
#2. Niezbędne statystyki do analizy danych od Udemy
Ten kurs Udemy uczy statystyki w praktyczny sposób, wykorzystując rzeczywiste projekty i ciekawe ćwiczenia. Omówione zostaną zagadnienia takie jak testowanie hipotez, rozkłady prawdopodobieństwa i analiza regresji.
#3. Statystyka dla nauki o danych i analizy biznesowej

Udemy oferuje również kurs statystyki dla analizy danych i biznesowej. Kurs ten umożliwia naukę testowania hipotez i innych tematów statystycznych. Jest skierowany do analityków danych i biznesowych, obejmuje statystykę opisową i wnioskową, a także analizę regresji.
#4. Testowanie hipotez autorstwa Jima Frosta
Książka Jima Frosta to intuicyjny przewodnik, który ułatwia analitykom podejmowanie decyzji opartych na danych.
Książka omawia mechanizmy testowania hipotez, uzasadnienie ich stosowania, oraz skuteczne wykorzystanie przedziałów ufności, wartości p i poziomów istotności.
#5. Testowanie hipotez Scotta Hartshorna
Ta książka wyróżnia się wizualnymi przykładami i jest doskonałym wyborem dla początkujących, którzy szukają zwięzłego wprowadzenia do testowania hipotez.
Książka zapoznaje czytelnika z podstawami statystyki, jej rodzajami i działaniem. Nie wymaga wcześniejszej dogłębnej wiedzy, a tematyka jest wyjaśniana w przystępny sposób.
Podsumowanie
Testowanie hipotez pomaga w weryfikacji założeń i wyciąganiu wniosków statystycznych na podstawie oceny danych. Jest wykorzystywane w wielu branżach, od produkcji, rolnictwa po badania kliniczne i IT. Metoda ta jest nie tylko precyzyjna, ale także pomaga w podejmowaniu decyzji w organizacjach na podstawie analizy danych.
Zachęcamy również do zapoznania się z dodatkowymi materiałami edukacyjnymi dla przyszłych analityków biznesowych.
newsblog.pl
Maciej – redaktor, pasjonat technologii i samozwańczy pogromca błędów w systemie Windows. Zna Linuxa lepiej niż własną lodówkę, a kawa to jego główne źródło zasilania. Pisze, testuje, naprawia – i czasem nawet wyłącza i włącza ponownie. W wolnych chwilach udaje, że odpoczywa, ale i tak kończy z laptopem na kolanach.