Algorytm Support Vector Machine, znany również jako SVM, to popularne narzędzie w dziedzinie uczenia maszynowego. Jego efektywność i zdolność do pracy z ograniczonymi zbiorami danych sprawiają, że jest szeroko stosowany. Ale czym właściwie jest SVM?
Czym jest maszyna wektorów nośnych (SVM)?
Maszyna wektorów nośnych to algorytm uczenia maszynowego, który opiera się na uczeniu nadzorowanym w celu stworzenia modelu klasyfikacji binarnej. Brzmi skomplikowanie? W tym artykule przybliżymy działanie SVM oraz jego zastosowanie w przetwarzaniu języka naturalnego. Zanim jednak przejdziemy do szczegółów, przyjrzyjmy się bliżej zasadzie działania SVM.
Jak działa SVM?
Wyobraźmy sobie prosty problem klasyfikacji, w którym mamy dane z dwoma cechami, oznaczonymi jako x i y, oraz jedną zmienną wyjściową – klasyfikację, która może przyjmować dwie wartości: „czerwony” lub „niebieski”. Dane te można przedstawić na wykresie w następujący sposób:
Naszym zadaniem jest stworzenie granicy decyzyjnej, czyli linii, która oddzieli od siebie obie klasy punktów danych. Poniżej znajduje się ten sam zestaw danych, ale z zaznaczoną granicą decyzyjną:
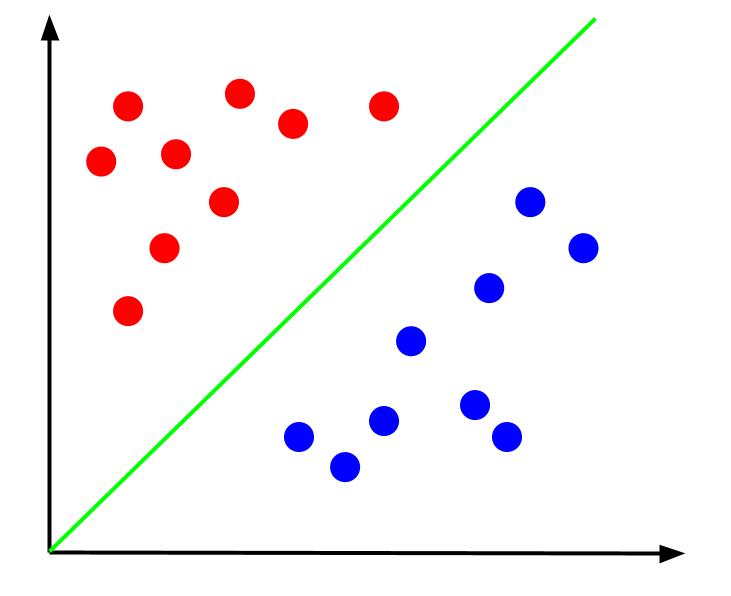
Dzięki tej granicy decyzyjnej, możemy przewidywać do której klasy należy dany punkt, na podstawie jego położenia względem granicy. Algorytm SVM tworzy optymalną granicę decyzyjną, która jest następnie wykorzystywana do klasyfikacji punktów.
Ale co rozumiemy przez „optymalną granicę decyzyjną”?
Można przyjąć, że optymalna granica decyzyjna to ta, która maksymalizuje swoją odległość od wektorów wsparcia. Wektory wsparcia to punkty danych z obu klas, które znajdują się najbliżej granicy. To one są najbardziej narażone na błędną klasyfikację ze względu na swoje bliskie sąsiedztwo z inną klasą.
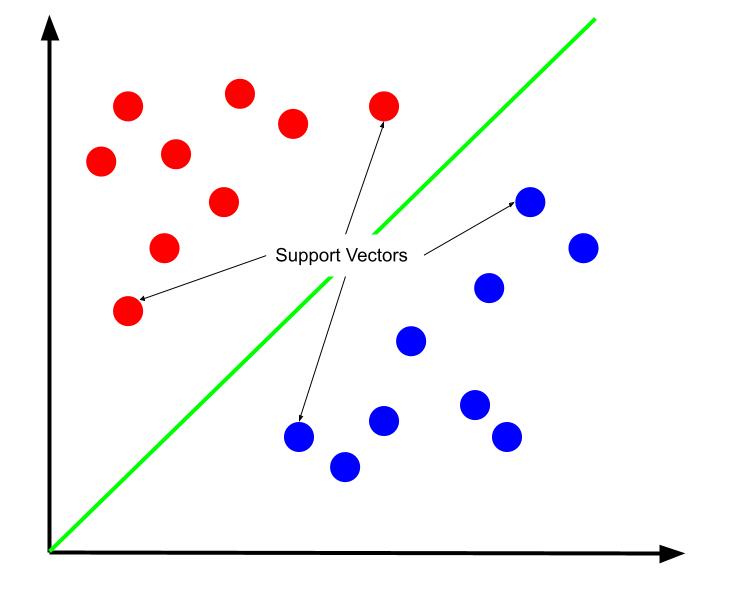
Uczenie maszyny wektorów nośnych polega zatem na poszukiwaniu linii, która maksymalizuje margines między wektorami wsparcia.
Ważne jest, aby pamiętać, że położenie granicy decyzyjnej jest wyznaczane wyłącznie przez wektory wsparcia. Pozostałe punkty danych nie mają na nią wpływu. W związku z tym, proces uczenia wymaga jedynie uwzględnienia wektorów wsparcia.
W naszym przykładzie, granica decyzyjna ma formę prostej linii. Jest to wynik tego, że nasz zbiór danych ma tylko dwie cechy. Jeśli danych cech jest trzy, granica decyzyjna przyjmuje formę płaszczyzny, a w przypadku czterech lub więcej cech – hiperpłaszczyzny.
Dane nierozdzielne liniowo
W powyższym przykładzie mieliśmy do czynienia z danymi, które można było oddzielić liniową granicą decyzyjną. Rozważmy teraz sytuację, w której dane przedstawiają się następująco:
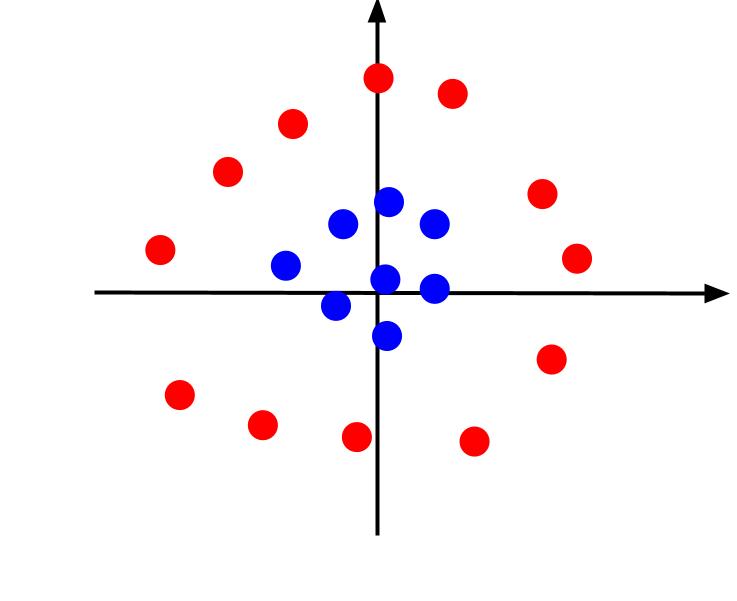
W tym przypadku nie jest możliwe rozdzielenie danych za pomocą prostej linii. Możemy jednak stworzyć dodatkową cechę, nazwijmy ją „z”, którą opisuje równanie: z = x^2 + y^2. Dodając „z” jako trzecią oś do płaszczyzny, uzyskujemy przestrzeń trójwymiarową.
Patrząc na wykres 3D pod takim kątem, że oś x jest pozioma, a oś z pionowa, otrzymamy widok podobny do tego:
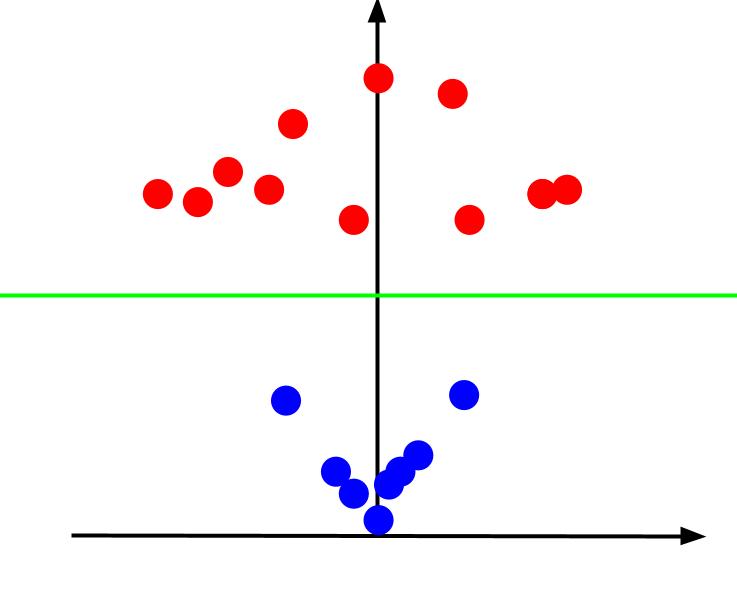
Wartość „z” informuje, jak daleko dany punkt znajduje się od początku układu względem innych punktów na starej płaszczyźnie XY. Niebieskie punkty, bliżej początku, mają niższe wartości „z”.
Natomiast czerwone punkty, dalej od początku, mają wyższe wartości „z”. Prezentując je w stosunku do wartości „z”, uzyskujemy czytelną klasyfikację, którą można oddzielić liniową granicą decyzyjną, jak pokazano na ilustracji.
Jest to kluczowa koncepcja wykorzystywana w maszynach wektorów nośnych. Ogólnie rzecz biorąc, chodzi o przekształcenie danych do przestrzeni o większej liczbie wymiarów, tak aby punkty danych mogły być oddzielone liniową granicą. Funkcje odpowiedzialne za to przekształcenie nazywamy funkcjami jądra. Istnieje wiele różnych funkcji jądra, np. sigmoidalna, liniowa, nieliniowa oraz RBF.
Aby mapowanie tych funkcji było bardziej wydajne, SVM wykorzystuje tzw. „sztuczkę jądra”.
SVM w uczeniu maszynowym
Maszyna wektorów nośnych to jeden z wielu algorytmów wykorzystywanych w uczeniu maszynowym. Obok popularnych drzew decyzyjnych i sieci neuronowych, SVM znajduje szerokie zastosowanie ze względu na swoją skuteczność, zwłaszcza przy mniejszej ilości danych. Jest często stosowany w takich zadaniach jak:
- Klasyfikacja tekstu: Uporządkowanie danych tekstowych, takich jak recenzje czy komentarze, w określone kategorie.
- Wykrywanie twarzy: Analiza obrazów w celu zidentyfikowania twarzy, na przykład w aplikacjach wykorzystujących rzeczywistość rozszerzoną.
- Klasyfikacja obrazów: Maszyny wektorów nośnych mogą efektywnie klasyfikować obrazy w porównaniu do innych metod.
Problem klasyfikacji tekstu
Internet jest pełen danych tekstowych. Wiele z tych danych jest jednak nieustrukturyzowanych i nieoznaczonych. Aby lepiej wykorzystać i zrozumieć te dane, konieczna jest ich klasyfikacja. Przykłady zastosowania klasyfikacji tekstu obejmują:
- Podział tweetów na tematy, aby ułatwić użytkownikom śledzenie interesujących ich kwestii.
- Kategoryzacja e-maili jako „Społeczności”, „Oferty” lub „Spam”.
- Klasyfikacja komentarzy na forach internetowych jako nienawistne lub obraźliwe.
Jak SVM współpracuje z klasyfikacją języka naturalnego
Maszyna wektorów nośnych jest wykorzystywana do klasyfikacji tekstu na ten, który pasuje do określonego tematu, i ten, który do niego nie pasuje. Odbywa się to poprzez przekształcenie danych tekstowych w zbiór danych z wieloma cechami.
Jedną z metod jest utworzenie cechy dla każdego słowa w zbiorze danych. Następnie, dla każdego punktu danych tekstowych, rejestrowana jest liczba wystąpień każdego słowa. Jeżeli w zbiorze danych występuje X unikalnych słów, wówczas otrzymamy X cech w zbiorze danych.
Dodatkowo, do tych punktów danych przypisywane są klasyfikacje. Chociaż te klasyfikacje są oznaczone tekstowo, większość implementacji SVM wymaga etykiet numerycznych.
Dlatego też, przed treningiem, konieczna jest konwersja etykiet tekstowych na liczby. Po przygotowaniu zestawu danych, wykorzystując te cechy jako współrzędne, model SVM może być użyty do klasyfikacji tekstu.
Tworzenie SVM w Pythonie
Do stworzenia maszyny wektorów nośnych (SVM) w Pythonie można użyć klasy SVC z biblioteki sklearn.svm. Poniżej znajduje się przykład wykorzystania klasy SVC do zbudowania modelu SVM:
from sklearn.svm import SVC
# Załaduj zbiór danych
X = ... y = ...
# Podziel dane na zbiory treningowe i testowe
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=19)
# Stwórz model SVM
model = SVC(kernel="linear")
# Wytrenuj model na danych treningowych
model.fit(X_train, y_train)
# Oceń model na danych testowych
accuracy = model.score(X_test, y_test)
print("Dokładność: ", accuracy)
W tym przykładzie, najpierw importujemy klasę SVC z biblioteki sklearn.svm. Następnie, ładujemy zbiór danych i dzielimy go na zbiory treningowe i testowe.
Następnie tworzymy model SVM, inicjalizując obiekt SVC i ustawiając parametr jądra na „liniowy”. Kolejno, trenujemy model na danych treningowych za pomocą metody „fit” i oceniamy go na danych testowych za pomocą metody „score”. Metoda „score” zwraca dokładność modelu, którą wyświetlamy w konsoli.
Można także określić inne parametry obiektu SVC, takie jak parametr C, który kontroluje siłę regularyzacji, oraz parametr gamma, który kontroluje współczynnik jądra dla niektórych jąder.
Korzyści z SVM
Oto lista niektórych zalet stosowania maszyn wektorów nośnych (SVM):
- Wydajność: SVM charakteryzują się wydajnością podczas trenowania, szczególnie przy dużej liczbie próbek.
- Odporność na szum: SVM są stosunkowo odporne na zakłócenia w danych treningowych, ponieważ dążą do znalezienia klasyfikatora maksymalnego marginesu, który jest mniej wrażliwy na szum niż inne klasyfikatory.
- Efektywność pamięciowa: SVM wymagają przechowywania w pamięci tylko podzbioru danych treningowych, co czyni je bardziej efektywnymi pod względem wykorzystania pamięci niż inne algorytmy.
- Skuteczność w przestrzeniach wielowymiarowych: SVM potrafią działać dobrze, nawet gdy liczba cech przekracza liczbę próbek.
- Wszechstronność: SVM mogą być stosowane w zadaniach klasyfikacji i regresji, a także mogą obsługiwać różne rodzaje danych, w tym dane liniowe i nieliniowe.
Teraz przyjrzyjmy się najlepszym zasobom do nauki maszyn wektorów nośnych (SVM).
Zasoby edukacyjne
Wprowadzenie do maszyn wektorów nośnych
Ta książka „Wprowadzenie do maszyn wektorów nośnych” kompleksowo i stopniowo wprowadza w metody uczenia oparte na jądrze.
Dostarcza solidne podstawy w teorii maszyn wektorów nośnych.
Zastosowania maszyn wektorów nośnych
Podczas gdy pierwsza książka skupiała się na teorii SVM, ta książka „Zastosowania maszyn wektorów nośnych” koncentruje się na ich praktycznych zastosowaniach.
Analizuje, jak SVM są wykorzystywane w przetwarzaniu obrazu, wykrywaniu wzorców i wizji komputerowej.
Maszyny wektorów nośnych (informatyka i statystyka)
Książka „Maszyny wektorów nośnych (informatyka i statystyka)” ma na celu przedstawienie przeglądu zasad leżących u podstaw skuteczności SVM w różnych zastosowaniach.
Autorzy zwracają uwagę na kilka czynników, które przyczyniają się do sukcesu SVM, w tym ich zdolność do dobrego działania przy ograniczonej liczbie regulowanych parametrów, ich odporność na różnego rodzaju błędy i anomalie oraz ich wydajność obliczeniową w porównaniu z innymi metodami.
Nauka z jądrami
„Nauka z jądrami” to książka, która wprowadza czytelników w działanie SVM i pokrewnych technik jądra.
Została stworzona, aby dać czytelnikom solidne podstawy matematyczne i wiedzę potrzebną do rozpoczęcia korzystania z algorytmów jądra w uczeniu maszynowym. Książka ma na celu dostarczenie dokładnego, ale przystępnego wprowadzenia do SVM i metod jądra.
Wsparcie maszyn wektorowych za pomocą Sci-kit Learn
Ten internetowy kurs „Support Vector Machines with Sci-kit Learn”, prowadzony przez sieć projektów Coursera, uczy, jak zaimplementować model SVM, korzystając z popularnej biblioteki uczenia maszynowego Sci-Kit Learn.
Dodatkowo poznasz teorię, która stoi za SVM, oraz określisz ich mocne strony i ograniczenia. Kurs jest na poziomie początkującym i trwa około 2,5 godziny.
Wsparcie Vector Machines w Pythonie: koncepcje i kod
Ten płatny kurs online na Udemy, „Maszyny wektorów pomocniczych w Pythonie”, obejmuje do 6 godzin instrukcji wideo i jest certyfikowany.
Obejmuje SVM i sposób ich solidnej implementacji w języku Python. Ponadto omawia biznesowe zastosowania maszyn wektorów nośnych.
Uczenie maszynowe i sztuczna inteligencja: obsługa maszyn wektorowych w języku Python
Na tym kursie „Uczenie maszynowe i sztuczna inteligencja”, nauczysz się, jak używać SVM do różnych praktycznych zastosowań, w tym do rozpoznawania obrazów, wykrywania spamu, diagnostyki medycznej i analizy regresji.
Będziesz wykorzystywać język programowania Python do implementacji modeli ML dla tych aplikacji.
Ostatnie słowa
W tym artykule krótko omówiliśmy teorię, która kryje się za maszynami wektorów nośnych. Zapoznaliśmy się z ich zastosowaniem w uczeniu maszynowym i przetwarzaniu języka naturalnego.
Zbadaliśmy także, jak wygląda ich implementacja przy użyciu scikit-learn. Ponadto, omówiliśmy praktyczne zastosowania i zalety SVM.
Chociaż ten artykuł był jedynie wprowadzeniem, dodatkowe zasoby oferują bardziej szczegółowe objaśnienia, dostarczając więcej informacji na temat maszyn wektorów nośnych. Ze względu na ich wszechstronność i wydajność, SVM warto zrozumieć, aby rozwijać się jako specjalista ds. danych i inżynier ML.
Następnie możesz sprawdzić najlepsze modele uczenia maszynowego.