Istnieją wątpliwości co do dokładności większości danych statystycznych – nawet przy przestrzeganiu procedur i stosowaniu wydajnego sprzętu do testowania. Program Excel umożliwia obliczanie niepewności na podstawie odchylenia standardowego próbki.
W programie Excel istnieją formuły statystyczne, których możemy użyć do obliczenia niepewności. W tym artykule obliczymy średnią arytmetyczną, odchylenie standardowe i błąd standardowy. Przyjrzymy się również, jak możemy wykreślić tę niepewność na wykresie w programie Excel.
W tych formułach użyjemy następujących przykładowych danych.
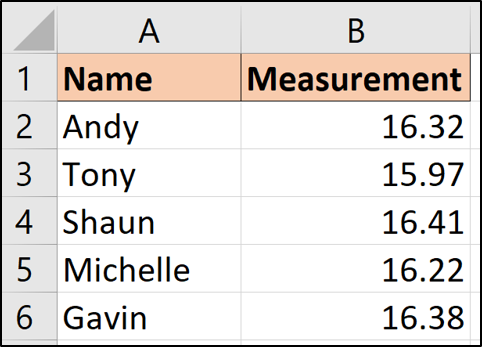
Te dane pokazują pięć osób, które dokonały jakiegoś pomiaru lub odczytu. Przy pięciu różnych odczytach nie mamy pewności, jaka jest rzeczywista wartość.
Spis treści:
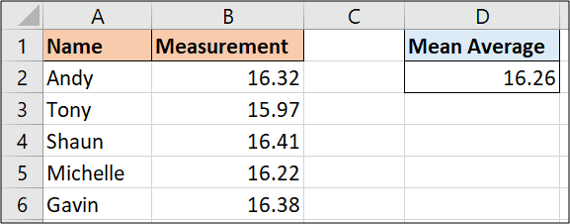
Średnia arytmetyczna wartości
W przypadku niepewności co do zakresu różnych wartości, przyjęcie średniej (średniej arytmetycznej) może posłużyć jako rozsądne oszacowanie.
Można to łatwo zrobić w programie Excel dzięki funkcji ŚREDNIA.
Na przykładowych danych powyżej możemy użyć następującego wzoru.
=AVERAGE(B2:B6)
Odchylenie standardowe wartości
Funkcje odchylenia standardowego pokazują, jak szeroko rozłożone są dane z centralnego punktu (średnia wartość średnia, którą obliczyliśmy w ostatniej sekcji).
Excel ma kilka różnych funkcji odchylenia standardowego do różnych celów. Dwa główne z nich to STDEV.P i STDEV.S.
Każdy z nich obliczy odchylenie standardowe. Różnica między nimi polega na tym, że ODCH.STANDARDOWE.Popiera się na dostarczeniu całej populacji wartości. ODCH.STANDARDOWE działa na mniejszej próbce tej populacji danych.
W tym przykładzie używamy wszystkich pięciu naszych wartości w zbiorze danych, więc będziemy pracować z ODCH. STANDARDOWE.
Ta funkcja działa w taki sam sposób jak ŚREDNIA. Możesz użyć poniższego wzoru na tej próbce danych.
=STDEV.P(B2:B6)
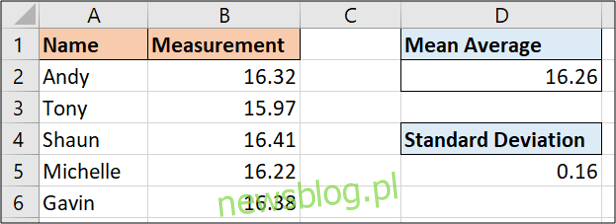
Wynik tych pięciu różnych wartości to 0,16. Ta liczba mówi nam, jak zwykle każdy pomiar różni się od wartości średniej.
Oblicz błąd standardowy
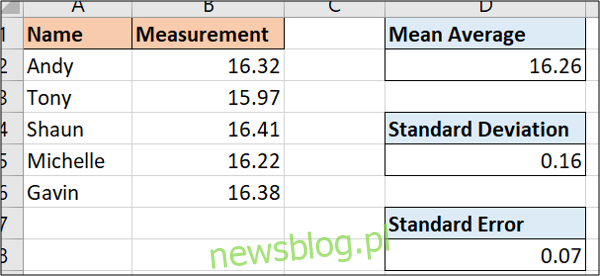
Po obliczeniu odchylenia standardowego możemy teraz znaleźć błąd standardowy.
Błąd standardowy to odchylenie standardowe podzielone przez pierwiastek kwadratowy z liczby pomiarów.
Poniższy wzór obliczy błąd standardowy na naszych przykładowych danych.
=D5/SQRT(COUNT(B2:B6))
Używanie słupków błędów do przedstawiania niepewności na wykresach
Excel sprawia, że wykreślanie odchyleń standardowych lub marginesów niepewności na wykresach jest cudownie proste. Możemy to zrobić, dodając słupki błędów.
Poniżej mamy wykres kolumnowy z przykładowego zestawu danych, przedstawiający populację mierzoną w ciągu pięciu lat.
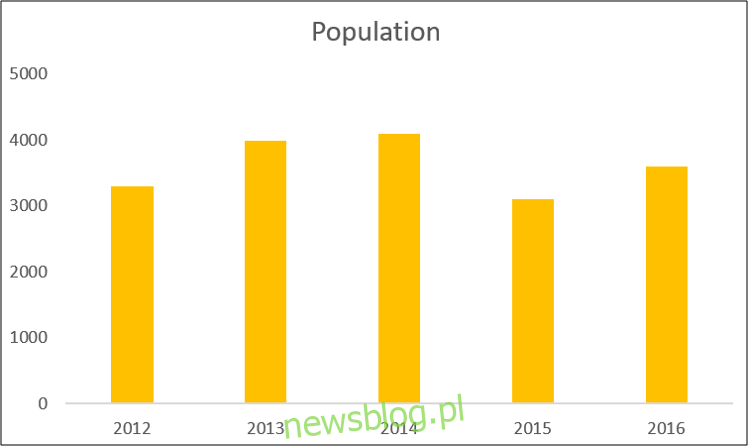
Po zaznaczeniu wykresu kliknij opcję Projekt> Dodaj element wykresu.
Następnie wybierz spośród różnych dostępnych typów błędów.
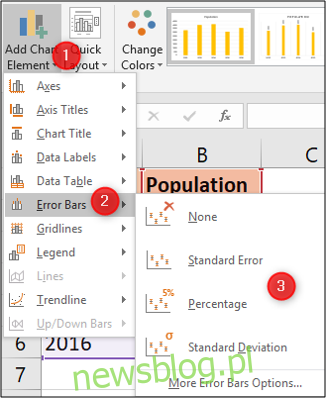
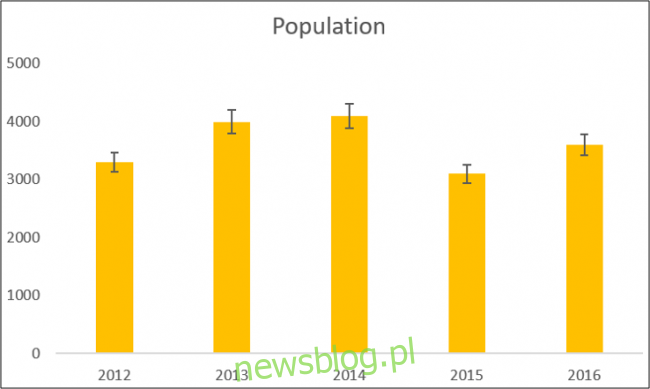
Możesz wyświetlić wartość błędu standardowego lub odchylenia standardowego dla wszystkich wartości, tak jak obliczyliśmy wcześniej w tym artykule. Możesz również wyświetlić procentową zmianę błędu. Wartość domyślna to 5%.
W tym przykładzie zdecydowaliśmy się pokazać procent.
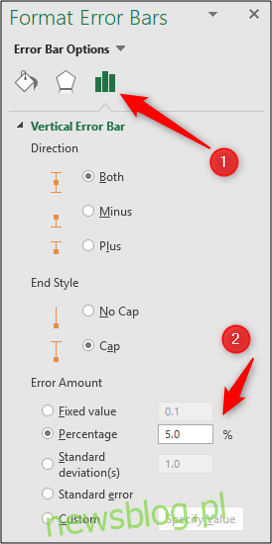
Istnieje kilka innych opcji do zbadania, aby dostosować paski błędów.
Kliknij dwukrotnie pasek błędów na wykresie, aby otworzyć okienko Formatowanie słupków błędów. Wybierz kategorię „Opcje słupków błędów”, jeśli nie jest jeszcze wybrana.
Następnie możesz dostosować wartość procentową, wartość odchylenia standardowego, a nawet wybrać wartość niestandardową z komórki, która mogła zostać utworzona przez formułę statystyczną.
Excel to idealne narzędzie do analizy statystycznej i raportowania. Zapewnia wiele sposobów obliczania niepewności, aby uzyskać to, czego potrzebujesz.